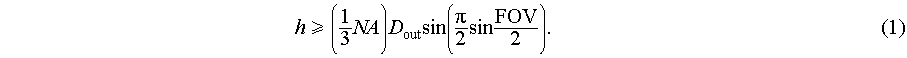| Issue |
Natl Sci Open
Volume 4, Number 6, 2025
Special Topic: Intelligent Materials and Devices
|
|
|---|---|---|
| Article Number | 20250038 | |
| Number of page(s) | 7 | |
| Section | Materials Science | |
| DOI | https://doi.org/10.1360/nso/20250038 | |
| Published online | 11 October 2025 | |
PERSPECTIVE
Nonlocal metasurfaces for next-generation flat optics
State Key Laboratory of Extreme Photonics and Instrumentation, College of Optical Science and Engineering, ZJU-Hangzhou Global Scientific and Technological Innovation Center, Zhejiang University, Hangzhou 310027, China
* Corresponding author (email: This email address is being protected from spambots. You need JavaScript enabled to view it.
)
Received:
7
August
2025
Revised:
29
September
2025
Accepted:
9
October
2025
The relentless pursuit of miniaturized, multifunctional photonic devices has elevated flat optics to a central position in contemporary photonics. A range of emerging trends is attracting significant research attention, including the progression of metasurface architectures from single-layer to multilayer configurations [1–3], the broadening of functionalities from achiral to chiral responses [4,5], and the shift from linear to nonlinear operation [6,7]. Particularly noteworthy is the expansion of metasurface design from local to nonlocal regimes, which plays a crucial role in shaping light with exceptional flexibility. This advancement has spurred numerous notable developments in critical application domains such as free-space compression, narrowband filtering and high-quality (high-Q) wavefront control, among others.
The definition of nonlocal metasurfaces can be elucidated by contrasting them with local metasurfaces, as illustrated in Figure 1a. In local metasurfaces, the electromagnetic response at any given spatial coordinate is determined solely by the incident field at that specific location. This results in a point-to-point relationship between input and output fields in real space, thereby producing a uniform response in momentum space. Conversely, in a nonlocal metasurface, the response at a particular point is influenced by the applied field over an extended spatial region, leading to a non-constant transfer function in momentum space [8]. This characteristic presents transformative development opportunities for metasurfaces.
 |
Figure 1 Some mechanisms and applications of nonlocal effects. (a) Physical diagram of local and nonlocal effect, both in real space and in momentum space (These are idealizations, as the response is never perfectly local) [8]. (b) Normalized distribution of the electric field amplitude for the focusing of a TE-polarized plane wave by a local idealized metalens, and the same metalens followed by nonlocal metasurfaces with 5 layers and 10 layers [14]. (c) Local and nonlocal meta-lenses are generally limited by broadband responses and circular polarization conversion efficiency TLR of ~25%, respectively. Nonlocal Huygens’ meta-lenses can simultaneously acquire narrowband wavefront shaping and efficiency TLR exceeding 25% [17]. Inset: tilted scanning electron microscope (SEM) image of the fabricated sample. The scale bar is 500 nm. (d) Schematic of the metalaser. Each unit cell is depicted as an inset. Here the lattice size of a unit cell is a = 360 nm. The radius and pillar height of the Si3N4 nanodisk are R = 135 nm and h = 150 nm, respectively [18]. The eccentric hole is positioned at L = 60 nm with a radius of r = 20 nm and variable rotation angle θ. With the control of the rotation angle of each hole, different laser profiles such as Gaussian beam, donut beam, focus spot, focus line, as well as hologram can be generated. The polarization angle θF of farfield radiation at the resonant wavelength as a function of rotation angle θ. Bottom insets show the electric field (left) and power (right) distributions of quasi-BIC in one unit cell. The top inset illustrates the geometric phase acquired by the emission from each Si3N4 nanodisk. |
From a physical perspective, such a response in momentum space corresponds to nonlocal resonances, also referred to as collective resonances. The pathways for their realization can be primarily categorized into two types of mechanisms: guided-mode resonances and quasi-bound states in the continuum (quasi-BIC). Different mechanisms for generating collective resonances are associated with distinct application scenarios, as detailed in the subsequent section. Furthermore, some studies [9,10] describe the adjacent electromagnetic coupling between meta-atoms within the nonlocality regime, which possesses significant application value. This concept differs fundamentally from the definition provided in this paper and is discussed and differentiated, alongside an introduction to the associated beyond-nearest-neighbour interactions [11,12]. Finally, the current challenges encountered by nonlocal metasurfaces are analyzed, and the potential opportunities they present for the advancement of next-generation planar optics are summarized.
Collective resonances: wavevector-dictated control via momentum space. Collective resonances suggest that the output point response of nonlocal metasurfaces is not isolated; rather, it results from the combined influence of an extensive area of the incident field, enabling the attainment of functionalities distinct from those of local metasurfaces. The core regulatory mechanism can be broadly categorized into two types: guided mode resonances and quasi-BIC resonances. Both types facilitate the modulation of momentum space.
Guided mode resonance (GMR) is a nonlocal lattice resonance phenomenon that utilizes periodic structures to induce the requisite spatial momentum displacement in the form of the lattice vector G. This mechanism effectively facilitates the coupling of transversely propagating waveguide modes into radiation diffraction orders, thereby fundamentally redirecting energy flow. These momentum-dependent nonlocal resonances provide novel insights for efficient free-space compression, given that the transfer function of free space is also momentum-dependent, a characteristic that cannot be replicated by conventional local flat optics with space-dependent transfer functions [13]. For small transverse wavevectors kt, the dispersion relation of guided mode resonance can be approximated as ω(kt) = ω0 + αkt2 (where ω0 and α represent the resonant frequency and the dispersion coefficient, respectively), which aligns with the phase delay characteristic of free space: {L-End}
 , where L denotes the length of free space. Based on this, Chen et al. [14] designed a 10-layer nonlocal metasurface (9λ0) to simulate 45λ0 of free-space propagation (Figure 1b), which has been verified to support wide-angle imaging. However, an increase in the compression ratio results in a reduction of the working angle and an enhancement of absorption loss due to strong guided mode localization, thereby limiting practical applications. Furthermore, GMR can be employed to achieve high-Q resonances, demonstrating significant potential for applications such as optical sensing, spectral filtering, and few-photon nonlinear optics [15,16]. For example, Fang et al. [16] have designed and experimentally demonstrated a million-scale ultrahigh-Q guided mode resonance at near-visible wavelengths in a resist-based etch-free metasurface. Under continuous wave laser pumping, they observed a narrowing of the linewidth associated with pump power at room temperature, indicating the potential of their meta-optics platform for controlling coherent quantum light sources.
, where L denotes the length of free space. Based on this, Chen et al. [14] designed a 10-layer nonlocal metasurface (9λ0) to simulate 45λ0 of free-space propagation (Figure 1b), which has been verified to support wide-angle imaging. However, an increase in the compression ratio results in a reduction of the working angle and an enhancement of absorption loss due to strong guided mode localization, thereby limiting practical applications. Furthermore, GMR can be employed to achieve high-Q resonances, demonstrating significant potential for applications such as optical sensing, spectral filtering, and few-photon nonlinear optics [15,16]. For example, Fang et al. [16] have designed and experimentally demonstrated a million-scale ultrahigh-Q guided mode resonance at near-visible wavelengths in a resist-based etch-free metasurface. Under continuous wave laser pumping, they observed a narrowing of the linewidth associated with pump power at room temperature, indicating the potential of their meta-optics platform for controlling coherent quantum light sources.
Bound states in the continuum represent a notable extension of the nonlocal resonance mechanism, characterized by distinct energy confinement in contrast to guided modes, which are typically classified into three categories including Friedrich-Wintgen BIC, symmetry-protected BIC (SP-BIC) and accidental BIC. By finely tuning system parameters such as introducing controlled symmetry breaking, one can generate quasi-BIC states, which provide essential support for nonlocal metasurfaces in high-Q light field control, facilitating applications like narrowband filtering, high-Q wavefront shaping and highly efficient photon-pair generation. For instance, Yao et al. [17] designed a nonlocal Huygens metalens that exploits quasi-BIC induced by structural asymmetry to achieve a high-Q resonance (Q ≈ 104), with a linewidth maintained below 0.1 nm at a designed wavelength of 1550 nm (Figure 1c). Another example is the metalaser proposed by Zeng et al. [18]. As depicted in Figure 1d, Si3N4 nanodisks with eccentric apertures generate quasi-BIC states, which are amplified via stimulated emission in gain media. Concurrently, a specific geometric phase is introduced through the rotation angle θ, facilitating high-Q wavefront manipulation; however, this also degrades the nonlocal resonant mode, consequently reducing the Q-factor of the metasurface to some extent. Furthermore, Zhang et al. [19] reported a metasurface that supports nonlocal resonances, enabled by the high-Q factors associated with quasi-BIC and other resonant modes. This configuration results in a substantial enhancement of the photon-pair generation rate by approximately 450 times compared to unpatterned LiNbO3 films. Additional experimental results pertaining to high-Q metasurfaces can be found in Table 1.
An experimental list of recent high-Q nonlocal resonance metasurfaces
Near-field coupling: nonlocal interactions via real space. In the preceding description, nonlocality is characterised as the modulation of the metasurface in momentum space; specifically, the output light field at a given point in real space is influenced by the distribution of the input light field across an extended region. It is important to highlight that in certain instances, the coupling between adjacent meta-atoms is also regarded as nonlocal. However, within the context of this definition, this coupling effect does not strictly conform to the classifications of local or nonlocal metasurfaces, as it neither satisfies the point-to-point response in real space nor facilitates the regulation of momentum space. A more suitable description would be to refer to it as a transitional state termed nonlocal interactions [9], which also plays a crucial role in the design of metasurfaces.
On the one hand, this nonlocal interaction will fundamentally reduce the predictive accuracy of the local response approximation (LRA) model employed in the design of local metasurfaces, as the structural characteristic length becomes comparable to the operating wavelength. In 2018, Lepeshov et al. [25] illustrated that the near-field coupling between Mie-resonant meta-atoms alters their individual magnetic responses, contingent upon their separation distances. On the other hand, utilizing and enhancing this coupling effect expands the design freedom to a certain extent including the coupling between transverse or longitudinal cells, which is typically integrated with inverse design methods [26,27]. For example, in 2020, Cai et al. [9] harnessed the strong interactions among nanoresonators to enhance the focusing efficiency of metalenses at 532 nm through a global evolutionary optimization methodology that accounts for the nonlocal interactions. The experimental results indicate improved efficiencies for thinner transmissive metalenses designed for visible light. Nevertheless, it is important to acknowledge that the capacity to reduce the thickness of metalens systems through nonlocal coupling between unit cells is not limitless. In 2022, Li and Hsu [28] conducted a theoretical analysis of the fundamental trade-off between the field of view (FOV) and the thickness of metalens systems. The Fourier transform duality between space and momentum indicates that an increase in angular diversity requires a greater degree of nonlocality (i.e., the lateral spread of incident waves), and thereby determines the device’s minimum thickness h by
This finding aligns closely with prior outcomes in metalens design [29,30].
Recently, an emerging concept known as beyond-nearest-neighbour interaction, a mechanism originally introduced in elastic and airborne acoustical metamaterials [11,12], has been employed to tailor unusual dispersion relations. The essence of this mechanism lies in the introduction of physical structures, which create energy transmission channels for beyond-nearest-neighbour units that do not typically interact. Utilizing this mechanism, Chen et al. [12] have realized roton-like acoustical dispersion relations, characterized by the emergence of a minimum value in the first Brillouin zone, by incorporating designed third nearest-neighbour interactions alongside the conventional nearest-neighbour interactions. Theoretically, analogous effects can be achieved in optics through the rational or inverse design of nonlocal coupling. However, achieving such dispersion relations necessitates a substantial number of nonlocal interaction rods or channels that must not overlap; otherwise, the interaction mechanism will be fundamentally altered [31], which inevitably leads to an increase in the system thickness [28,32]. The aforementioned work by Chen et al. [12] has also been implemented in three-dimensional metamaterials, further substantiating the limitations imposed by thickness.
Application challenges and future outlook. Despite the transformative potential, the utilization of nonlocal metasurfaces encounters significant challenges, due to the increased complexity of design and theoretical modeling as well as the stringent requirements for fabrication precision. Nonlocal responses are influenced by intrinsic material dispersion and structural parameters, such as unit geometry and arrangement, both of which demonstrate dependence on frequency and wavevector. This situation necessitates the simultaneous optimization of unit geometry, periodic arrangement, and material dispersion, thereby exacerbating the overall design complexity. Established effective medium models for quantitative prediction and optimization of nonlocal effects remain underdeveloped, particularly for complex aperiodic structures [32]. Furthermore, artificially engineered nonlocal effects, particularly for high-Q resonances, require stringent fabrication precision to ensure their stability; even nanometre-scale variations in unit placement or shape can catastrophically degrade coupling precision and device performance. Consequently, this imposes heightened demands on nanofabrication technologies. There is an urgent need for robust inverse design frameworks and automated optimization strategies that connect nonlocal theories with fabrication constraints.
Future advancements in nonlocal theoretical modeling and advanced micro/nanofabrication are set to unlock significant potential for nonlocal metasurfaces. Firstly, the exploitation of nonlocality will facilitate the development of multifunctional or ultra-compact optical systems, significantly reducing the footprint of complex optical devices such as those targeting narrowband filtering and high-Q wavefront shaping. Secondly, optimized metasurface designs will enable precise control over the coupling of light fields which is anticipated to decrease overall thickness of the imaging systems, notwithstanding the theoretical limitations discussed in Ref. [28]. Furthermore, these metasurfaces are poised to function not merely as components but as fully integrated platforms for quantum photonics. They could seamlessly incorporate on-demand entangled quantum light sources, optical signal modulation elements, and photon-pair generation functionalities. Consequently, nonlocal metasurfaces and metalenses are positioned to become pivotal drivers of transformative advances in flat optics. This trajectory effectively connects fundamental research in nanophotonics and quantum physics with practical engineering applications, thereby establishing robust foundations for the next generation of multifunctional and miniaturized optical innovations.
Acknowledgments
The authors would like to acknowledge Weige Lv, Liying Chen and Wei Wang from the State Key Laboratory for Extreme Photonics and Instrumentation and College of Optical Science and Engineering, Zhejiang University for their assistance.
Funding
This work was supported by the STI 2030-Major Projects (2021ZD0200401), the National Natural Science Foundation of China (62222511), the Natural Science Foundation of Zhejiang Province (LR22F050006), and the National Key Research and Development Program of China (2023YFF0613000).
Author contributions
Y.M. proposed the topic of the perspective. S.T. wrote the manuscript and designed the figures. Y.M. and S.T. reviewed, edited and revised the manuscript.
Conflict of interest
The authors declare no conflict of interest.
References
- Arbabi A, Arbabi E, Kamali SM, et al. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat Commun 2016; 7: 13682. [Article] [Google Scholar]
- Avayu O, Almeida E, Prior Y, et al. Composite functional metasurfaces for multispectral achromatic optics. Nat Commun 2017; 8: 14992. [Article] [Google Scholar]
- Zhou Y, Kravchenko II, Wang H, et al. Multilayer noninteracting dielectric metasurfaces for multiwavelength metaoptics. Nano Lett 2018; 18: 7529-7537. [Article] [Google Scholar]
- Han Z, Wang F, Sun J, et al. Recent advances in ultrathin chiral metasurfaces by twisted stacking. Adv Mater 2023; 35: 2206141. [Article] [Google Scholar]
- Hu Z, Sun Y, Dong H, et al. Recent advances in dielectric chiral metasurfaces. Adv Phys Res 2025; 4: 2400187. [Article] [Google Scholar]
- Krasnok A, Tymchenko M, Alù A. Nonlinear metasurfaces: A paradigm shift in nonlinear optics. Mater Today 2018; 21: 8-21. [Article] [Google Scholar]
- Fan Y, Liang H, Li J, et al. Emerging trend in unconventional metasurfaces: From nonlinear, non-hermitian to nonclassical metasurfaces. ACS Photonics 2022; 9: 2872-2890. [Article] [Google Scholar]
- Shastri K, Monticone F. Nonlocal flat optics. Nat Photon 2023; 17: 36-47. [Article] [Google Scholar]
- Cai H, Srinivasan S, Czaplewski DA, et al. Inverse design of metasurfaces with non-local interactions. npj Comput Mater 2020; 6: 116. [Article] [Google Scholar]
- Isnard E, Héron S, Lanteri S, et al. Advancing wavefront shaping with resonant nonlocal metasurfaces: Beyond the limitations of lookup tables. Sci Rep 2024; 14: 1555. [Article] [Google Scholar]
- Chen Y, Fleury R, Seppecher P, et al. Nonlocal metamaterials and metasurfaces. Nat Rev Phys 2025; 7: 299-312. [Article] [Google Scholar]
- Chen Y, Kadic M, Wegener M. Roton-like acoustical dispersion relations in 3D metamaterials. Nat Commun 2021; 12: 3278. [Article] [Google Scholar]
- Guo C, Wang H, Fan S. Squeeze free space with nonlocal flat optics. Optica 2020; 7: 1133-1138. [Article] [CrossRef] [Google Scholar]
- Chen A, Monticone F. Dielectric nonlocal metasurfaces for fully solid-state ultrathin optical systems. ACS Photonics 2021; 8: 1439-1447. [Article] [CrossRef] [Google Scholar]
- Huang L, Jin R, Zhou C, et al. Ultrahigh-Q guided mode resonances in an all-dielectric metasurface. Nat Commun 2023; 14: 3433. [Article] [Google Scholar]
- Fang J, Chen R, Sharp D, et al. Million-Q free space meta-optical resonator at near-visible wavelengths. Nat Commun 2024; 15: 10341. [Article] [Google Scholar]
- Yao J, Lai F, Fan Y, et al. Nonlocal meta-lens with Huygens’ bound states in the continuum. Nat Commun 2024; 15: 6543. [Article] [Google Scholar]
- Zeng Y, Sha X, Zhang C, et al. Metalasers with arbitrarily shaped wavefront. Nature 2025; 643: 1240-1245. [Article] [Google Scholar]
- Zhang J, Ma J, Parry M, et al. Spatially entangled photon pairs from lithium niobate nonlocal metasurfaces. Sci Adv 2022; 8: eabq4240. [Article] [Google Scholar]
- Li Z, Zhou L, Liu Z, et al. Modifying the quality factors of the bound states in the continuum in a dielectric metasurface by mode coupling. ACS Photonics 2023; 10: 206-216. [Article] [Google Scholar]
- Liu Z, Xu Y, Lin Y, et al. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys Rev Lett 2019; 123: 253901. [Article] [Google Scholar]
- Fang CZ, Yang QY, Yuan QC, et al. High-Q resonances governed by the quasi-bound states in the continuum in all-dielectric metasurfaces. OEA 2021; 4: 200030. [Article] [Google Scholar]
- Watanabe K, Nagao T, Iwanaga M. Low-contrast BIC metasurfaces with quality factors exceeding 100,000. Nano Lett 2025; 25: 2777-2784. [Article] [Google Scholar]
- Huang L, Li S, Zhou C, et al. Realizing ultrahigh-Q resonances through harnessing symmetry-protected bound states in the continuum. Adv Funct Mater 2024; 34: 2309982. [Article] [Google Scholar]
- Lepeshov S, Kivshar Y. Near-field coupling effects in mie-resonant photonic structures and all-dielectric metasurfaces. ACS Photonics 2018; 5: 2888-2894. [Article] [Google Scholar]
- Li M, Zhang Y, Ma Z. Deep-learning-based metasurface design method considering near-field couplings. IEEE J Multiscale Multiphys Comput Tech 2023; 8: 40-48. [Article] [Google Scholar]
- Mansouree M, Kwon H, Arbabi E, et al. Multifunctional 2.5D metastructures enabled by adjoint optimization. Optica 2020; 7: 77-84. [Article] [CrossRef] [Google Scholar]
- Li S, Hsu CW. Thickness bound for nonlocal wide-field-of-view metalenses. Light Sci Appl 2022; 11: 338. [Article] [Google Scholar]
- Lin Z, Groever B, Capasso F, et al. Topology-optimized multilayered metaoptics. Phys Rev Appl 2018; 9: 044030. [Article] [Google Scholar]
- Lin Z, Roques-Carmes C, Christiansen RE, et al. Computational inverse design for ultra-compact single-piece metalenses free of chromatic and angular aberration. Appl Phys Lett 2021; 118: 041104. [Article] [Google Scholar]
- Wang K, Chen Y, Kadic M, et al. Nonlocal interaction engineering of 2D roton-like dispersion relations in acoustic and mechanical metamaterials. Commun Mater 2022; 3: 35. [Article] [Google Scholar]
- Monticone F, Mortensen NA, Fernández-Domínguez AI, et al. Nonlocality in photonic materials and metamaterials: Roadmap. Opt Mater Express 2025; 15: 1544. [Article] [Google Scholar]
© The Author(s) 2025. Published by Science Press and EDP Sciences.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
All Tables
All Figures
 |
Figure 1 Some mechanisms and applications of nonlocal effects. (a) Physical diagram of local and nonlocal effect, both in real space and in momentum space (These are idealizations, as the response is never perfectly local) [8]. (b) Normalized distribution of the electric field amplitude for the focusing of a TE-polarized plane wave by a local idealized metalens, and the same metalens followed by nonlocal metasurfaces with 5 layers and 10 layers [14]. (c) Local and nonlocal meta-lenses are generally limited by broadband responses and circular polarization conversion efficiency TLR of ~25%, respectively. Nonlocal Huygens’ meta-lenses can simultaneously acquire narrowband wavefront shaping and efficiency TLR exceeding 25% [17]. Inset: tilted scanning electron microscope (SEM) image of the fabricated sample. The scale bar is 500 nm. (d) Schematic of the metalaser. Each unit cell is depicted as an inset. Here the lattice size of a unit cell is a = 360 nm. The radius and pillar height of the Si3N4 nanodisk are R = 135 nm and h = 150 nm, respectively [18]. The eccentric hole is positioned at L = 60 nm with a radius of r = 20 nm and variable rotation angle θ. With the control of the rotation angle of each hole, different laser profiles such as Gaussian beam, donut beam, focus spot, focus line, as well as hologram can be generated. The polarization angle θF of farfield radiation at the resonant wavelength as a function of rotation angle θ. Bottom insets show the electric field (left) and power (right) distributions of quasi-BIC in one unit cell. The top inset illustrates the geometric phase acquired by the emission from each Si3N4 nanodisk. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.