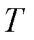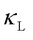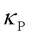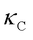| Issue |
Natl Sci Open
Volume 4, Number 3, 2025
Special Topic: Thermoelectric Materials and Devices
|
|
|---|---|---|
| Article Number | 20250007 | |
| Number of page(s) | 3 | |
| Section | Materials Science | |
| DOI | https://doi.org/10.1360/nso/20250007 | |
| Published online | 24 March 2025 | |
PERSPECTIVE
Thermal conductivity of solids from lattice dynamics
Department of Mechanical Engineering, The University of Hong Kong, Hong Kong 999077, China
* Corresponding authors (emails: u3004964@connect.hku.hk (Zezhu Zeng); yuechen@hku.hk (Yue Chen))
Received:
28
February
2025
Revised:
17
March
2025
Accepted:
20
March
2025
Heat transport is a fundamental process underlying both natural phenomena and technological advancements. In semiconductors and insulators, where heat is primarily carried by lattice vibrations, the lattice thermal conductivity (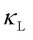 ) plays a crucial role in governing thermal transport. Lattice dynamics provides a robust theoretical framework for calculating
) plays a crucial role in governing thermal transport. Lattice dynamics provides a robust theoretical framework for calculating 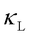 , with different approaches tailored to the structural and morphological characteristics of materials.
, with different approaches tailored to the structural and morphological characteristics of materials.
Solids can be broadly classified into crystals, glasses, and partially disordered solids, with a continuous crossover between these categories (see Figure 1). In crystalline semiconductors and insulators, heat is primarily carried by phonons. The phonon-gas model (PGM), introduced by Peierls in 1929, reliably predicts 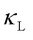 in simple crystals, ranging from ~1000 W/mK for boron arsenide to 0.9 W/mK for silver chloride at 300 K. In glasses, strong atomic disorder breaks down the phonon definition, making the PGM unsuitable for computing glassy
in simple crystals, ranging from ~1000 W/mK for boron arsenide to 0.9 W/mK for silver chloride at 300 K. In glasses, strong atomic disorder breaks down the phonon definition, making the PGM unsuitable for computing glassy 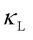 . To address this, Allen and Feldman [1] proposed the AF model in 1993, which describes the glassy heat transport in harmonic glasses through Zener-like tunneling between quasi-degenerate vibrational eigenstates.
. To address this, Allen and Feldman [1] proposed the AF model in 1993, which describes the glassy heat transport in harmonic glasses through Zener-like tunneling between quasi-degenerate vibrational eigenstates.
 |
Figure 1 Classification of solids and their heat transport mechanisms. The left panel categorizes solids based on atomic disorder, ranging from simple and complex crystals through partially disordered solids to glasses. The corresponding vibrational power spectra illustrate the transition from well-separated phonon modes in simple crystals to overlapping modes in complex crystals due to phonon broadening. The right panel depicts the typical temperature ( |
However, exceptions to these models exist. In certain complex crystals with glass-like heat conduction, such as Tl3VSe4 [2], severe phonon scattering reduces the phonon mean free path below the minimum interatomic spacing, significantly limiting phonon propagation. As a result, 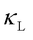 of Tl3VSe4 computed using the PGM substantially underestimates experimental results [2]. Moreover, the transition from crystals to glasses is nonsharp, with partially disordered materials [3] occupying an intermediate regime where heat transport cannot be accurately described by either the PGM or the AF model.
of Tl3VSe4 computed using the PGM substantially underestimates experimental results [2]. Moreover, the transition from crystals to glasses is nonsharp, with partially disordered materials [3] occupying an intermediate regime where heat transport cannot be accurately described by either the PGM or the AF model.
In 2019, Simoncelli et al. [4] introduced the Wigner transport equation (WTE) to describe heat conduction in solids, incorporating both intraband propagation (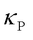 ) and interband coherence (
) and interband coherence (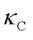 ) via Zener-like tunneling. This framework unifies particle-like phonon propagation (dominant in crystals) and wavelike phonon coherence (dominant in glasses), and the overall
) via Zener-like tunneling. This framework unifies particle-like phonon propagation (dominant in crystals) and wavelike phonon coherence (dominant in glasses), and the overall 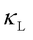 is the summation of
is the summation of 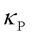 and
and 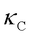 . Later, Isaeva et al. [5] developed the Quasi-harmonic Green-Kubo theory (QHGK), which is also applicable to both crystalline and glassy solids. A detailed comparison between WTE and QHGK can be found in previous studies [6, 7].
. Later, Isaeva et al. [5] developed the Quasi-harmonic Green-Kubo theory (QHGK), which is also applicable to both crystalline and glassy solids. A detailed comparison between WTE and QHGK can be found in previous studies [6, 7].
Specifically, in simple crystals with moderate anharmonicity, where 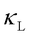 typically follows a
typically follows a 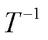 dependence, WTE and QHGK predict that the heat transport is dominated by particle-like phonon propagation, with wave-like tunneling effects being negligible. In contrast, in complex crystals with strong anharmonicity, where closely spaced vibrational frequencies and large phonon linewidths lead to significant phonon mode overlap (see Figure 1), WTE and QHGK predict a substantial interband coherence contribution (
dependence, WTE and QHGK predict that the heat transport is dominated by particle-like phonon propagation, with wave-like tunneling effects being negligible. In contrast, in complex crystals with strong anharmonicity, where closely spaced vibrational frequencies and large phonon linewidths lead to significant phonon mode overlap (see Figure 1), WTE and QHGK predict a substantial interband coherence contribution (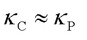 ), resulting in glass-like
), resulting in glass-like 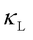 with a weakened
with a weakened 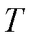 -dependence. In extreme cases, where
-dependence. In extreme cases, where 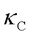 dominates heat transport in crystals,
dominates heat transport in crystals, 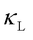 can even increase with temperature.
can even increase with temperature.
For partially disordered solids and glasses, calculating 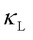 requires sufficiently large atomistic models to capture atomic disorder. Once the model is large enough to represent the amorphous structure, further increases in system size or changes in boundary conditions have minimal impact on
requires sufficiently large atomistic models to capture atomic disorder. Once the model is large enough to represent the amorphous structure, further increases in system size or changes in boundary conditions have minimal impact on 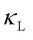 . Therefore, computing
. Therefore, computing 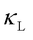 for disordered solids is computationally expensive and labor-intensive. To overcome this challenge, the regularized WTE (rWTE) approach [8] was developed to accelerate
for disordered solids is computationally expensive and labor-intensive. To overcome this challenge, the regularized WTE (rWTE) approach [8] was developed to accelerate 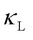 calculations in strongly disordered glasses by using a relatively small atomic model with Fourier interpolation. This method is particularly effective when disorder-induced repulsion between vibrational energy levels is comparable to the intrinsic linewidths from phonon-phonon scattering or isotopic scattering.
calculations in strongly disordered glasses by using a relatively small atomic model with Fourier interpolation. This method is particularly effective when disorder-induced repulsion between vibrational energy levels is comparable to the intrinsic linewidths from phonon-phonon scattering or isotopic scattering.
Although WTE and QHGK are powerful tools for assessing heat transport in solids, they have inherent challenges and limitations. A key challenge arises in glasses, where the interplay between anharmonicity and disorder complicates the convergence of 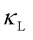 . The AF model predicts a finite
. The AF model predicts a finite 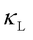 for harmonic glasses at low temperatures. However, Fiorentino et al. [9] emphasized that incorporating anharmonic linewidths in QHGK is essential for achieving convergence. Recent studies [10] have shown that
for harmonic glasses at low temperatures. However, Fiorentino et al. [9] emphasized that incorporating anharmonic linewidths in QHGK is essential for achieving convergence. Recent studies [10] have shown that 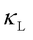 can converge in harmonic disordered systems if the disorder is not simple white-noise mass disorder and the disorder-induced phonon lifetimes deviate from Rayleigh scattering at low frequencies. We emphasize that further research is needed to better understand the interplay between atomic disorder (nearly
can converge in harmonic disordered systems if the disorder is not simple white-noise mass disorder and the disorder-induced phonon lifetimes deviate from Rayleigh scattering at low frequencies. We emphasize that further research is needed to better understand the interplay between atomic disorder (nearly 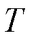 -independent) and anharmonicity (
-independent) and anharmonicity (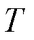 -dependent) in glasses.
-dependent) in glasses.
WTE and QHGK have limitations in their applicability. Both methods require phonons to be well-defined quasiparticles, meaning their linewidths must be smaller than their energies. This assumption breaks down in strongly anharmonic solids with ultralow 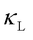 , where phonon linewidths become comparable to or exceed their energies. Similarly, in halide perovskites with low-frequency overdamped modes, the phonon power spectrum deviates significantly from a Lorentzian shape, exhibiting imaginary frequencies that render linewidth extraction unreliable. In such cases, the full phonon spectral function method [6] on top of WTE may provide a more accurate prediction of
, where phonon linewidths become comparable to or exceed their energies. Similarly, in halide perovskites with low-frequency overdamped modes, the phonon power spectrum deviates significantly from a Lorentzian shape, exhibiting imaginary frequencies that render linewidth extraction unreliable. In such cases, the full phonon spectral function method [6] on top of WTE may provide a more accurate prediction of 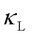 .
.
Additionally, WTE and QHGK assume that atoms vibrate around well-defined equilibrium positions (i.e., need a stable initial atomic model to compute 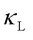 ). However, this assumption often fails in metastable materials with frequent atomic hopping and spinning or in phase-change materials transitioning between amorphous and crystalline states. These materials feature a complex energy landscape with multiple metastable states, resulting in dynamic atomic rearrangements. Accurately modeling heat transport in such systems requires more advanced computational approaches beyond existing methods.
). However, this assumption often fails in metastable materials with frequent atomic hopping and spinning or in phase-change materials transitioning between amorphous and crystalline states. These materials feature a complex energy landscape with multiple metastable states, resulting in dynamic atomic rearrangements. Accurately modeling heat transport in such systems requires more advanced computational approaches beyond existing methods.
Challenges and opportunities coexist. The recent advancements in machine learning and artificial intelligence are making the implementation and application of existing heat transport theories increasingly feasible. Future efforts may focus on developing more general theoretical frameworks to address unconventional and unresolved heat transport phenomena across diverse materials. We anticipate that emerging heat transport theories will continue to deepen our understanding of transport mechanisms in complex systems, such as solid-liquid interfaces and supercooled glasses.
References
- Allen PB, Feldman JL. Thermal conductivity of disordered harmonic solids. Phys Rev B 1993; 48: 12581–12588.[Article] [Google Scholar]
- Mukhopadhyay S, Parker DS, Sales BC, et al. Two-channel model for ultralow thermal conductivity of crystalline Tl3VSe4. Science 2018; 360: 1455–1458.[Article] [Google Scholar]
- Simonov A, Goodwin AL. Designing disorder into crystalline materials. Nat Rev Chem 2020; 4: 657–673.[Article] [Google Scholar]
- Simoncelli M, Marzari N, Mauri F. Unified theory of thermal transport in crystals and glasses. Nat Phys 2019; 15: 809–813.[Article] [Google Scholar]
- Isaeva L, Barbalinardo G, Donadio D, et al. Modeling heat transport in crystals and glasses from a unified lattice-dynamical approach. Nat Commun 2019; 10: 3853.[Article] [Google Scholar]
- Caldarelli G, Simoncelli M, Marzari N, et al. Many-body Green's function approach to lattice thermal transport. Phys Rev B 2022; 106: 024312.[Article] [CrossRef] [PubMed] [Google Scholar]
- Simoncelli M, Marzari N, Mauri F. Wigner formulation of thermal transport in solids. Phys Rev X 2022; 12: 041011.[Article] [Google Scholar]
- Simoncelli M, Mauri F, Marzari N. Thermal conductivity of glasses: First-principles theory and applications. npj Comput Mater 2023; 9: 106.[Article] [Google Scholar]
- Fiorentino A, Drigo E, Baroni S, et al. Unearthing the foundational role of anharmonicity in heat transport in glasses. Phys Rev B 2024; 109: 224202.[Article] [CrossRef] [Google Scholar]
- Fiorentino A, Pegolo P, Baroni S, et al. Effects of colored disorder on the heat conductivity of SiGe alloys from first principles. arXiv: https://arxiv.org/abs/2408.051552408.05155 [Google Scholar]
© The Author(s) 2025. Published by Science Press and EDP Sciences.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0">https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0">https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
All Figures
 |
Figure 1 Classification of solids and their heat transport mechanisms. The left panel categorizes solids based on atomic disorder, ranging from simple and complex crystals through partially disordered solids to glasses. The corresponding vibrational power spectra illustrate the transition from well-separated phonon modes in simple crystals to overlapping modes in complex crystals due to phonon broadening. The right panel depicts the typical temperature ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.