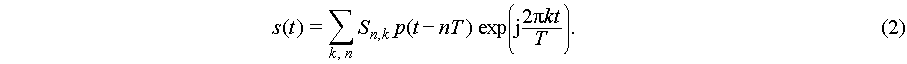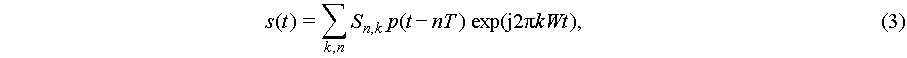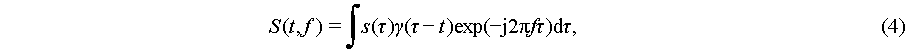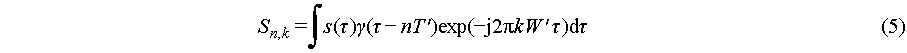| Issue |
Natl Sci Open
Volume 4, Number 6, 2025
|
|
|---|---|---|
| Article Number | 20250047 | |
| Number of page(s) | 5 | |
| Section | Information Sciences | |
| DOI | https://doi.org/10.1360/nso/20250047 | |
| Published online | 20 October 2025 | |
PERSPECTIVE
Recall Gabor communication theory and joint time-frequency analysis
Department of Electrical and Computer Engineering, University of Delaware, Newark, DE 19716, USA
* Corresponding author (email: This email address is being protected from spambots. You need JavaScript enabled to view it.
)
Received:
12
September
2025
Revised:
14
October
2025
Accepted:
16
October
2025
In the 1940s, there were two major concepts about digital communications. One was by Claude Shannon, i.e., the well-known Shannon communication theory published in the 1948 Bell System Technical Journal, which has become the foundation in modern digital communications. This is very well known these days and I will not elaborate any more about it here. The other was by Gabor [1] who published “Theory of communication. Part 1: The analysis of information” in 1946. In comparison, Shannon’s theory is more from statistical point of view and more mathematical, while Gabor’s theory is more from structural or deterministic point of view and more physical, and also from more system view point. I will try to elaborate Gabor’s communication theory a little more below.
In Gabor’s communication theory, digital transmission is basically to tile the time and frequency plane. Given a time and frequency plane (or a channel), how many atoms (called Gabor atoms) can be packed and separated in the plane is a kind of the physical capacity of the channel. The smaller the atoms are, the larger the capacity is, i.e., more different signals can be separated/detected. In other words, the smaller the product of the band width and time width is, the larger the capacity is. Unfortunately, due to Heisenberg’s uncertainty principle, the minimum product of the band width and the time width is 1/2, which in fact provides the physical capacity for a given time and frequency plane, no matter single or multi-user communication systems. This is the fundamental limit in physics and unfortunately, these days, many people have forgotten this fundamental physics limit. I think that a key difference with Shannon communication theory is that in Gabor’s framework, the discrete signals Sn and Sn,k below are not necessarily quantized, i.e., not necessary in bits, and I think that it might be better to call Gabor’s as semi-digital.
Since Gaussian pulse p(t) = aexp(−bt2) for non-zero constants a and b > 0 reaches the lower bound 1/2 of the product of the band width and time width, Gaussian pulse is the most compact pulse (or the most time-frequency localized pulse) in the product domain of time and frequency. This is the reason why it is used in the following transmission signal
where Sn are the digital symbols to transmit and T is the time duration of a digital symbol to transmit. In fact, it is the reason why Gaussian pulse is used in the 2G GSM standard. The transmission signal in Eq. (1) is only in time domain. If it is tiled in both time and frequency domains, the signal becomes
It is the formula (1.29) in Ref. [1], where p(t) is the Gaussian pulse. In other words, in terms of the time and frequency tilings, no pulse is better than the Gaussian pulse, no matter it is single or multi-user communication system, for a given time and frequency rectangular area in the time and frequency plane.
In fact, the frequency shift 1/T in Eq. (2) can be generalized to a general W as
under the condition {L-End}
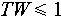 , where the functions pn,k(t) = p(t−nT)exp(j2πkW) for integers n and k are called Gabor atoms. The condition {L-End}
, where the functions pn,k(t) = p(t−nT)exp(j2πkW) for integers n and k are called Gabor atoms. The condition {L-End}
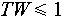 on the sampling symbol time interval length T and the sampling frequency bandwidth W is to ensure that the signal can be uniquely demodulated/recovered at the receiver. From this condition, T = 1/W used in Eq. (2) is the maximum sampling interval length for a given sampling bandwidth W.
on the sampling symbol time interval length T and the sampling frequency bandwidth W is to ensure that the signal can be uniquely demodulated/recovered at the receiver. From this condition, T = 1/W used in Eq. (2) is the maximum sampling interval length for a given sampling bandwidth W.
The transmission signal (2) is a special case of Eq. (3) when W = 1/T. If we sample time variable t in Eq. (3) and use the rectangular pulse, i.e., p(t) is the rectangular pulse of length T, for example, t = i, T = N and W = 1/N, Eq. (3) is an OFDM signal without cyclic prefix (CP), where k, {L-End}
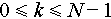 , is the subcarrier index, W is the subcarrier spacing, and n is the orthogonal frequency division multiplexing (OFDM) symbol index. If p(t) is a more general pulse, Eq. (3) is generalized OFDM (GFDM), which corresponds to the inverse discrete Gabor transform (DGT) below. This means that both mathematical forms of OFDM and GFDM may be traced back to Gabor’s 1946 paper [1].
, is the subcarrier index, W is the subcarrier spacing, and n is the orthogonal frequency division multiplexing (OFDM) symbol index. If p(t) is a more general pulse, Eq. (3) is generalized OFDM (GFDM), which corresponds to the inverse discrete Gabor transform (DGT) below. This means that both mathematical forms of OFDM and GFDM may be traced back to Gabor’s 1946 paper [1].
Also as one can see from the above, using pulses in signal transmission appeared from the very beginning of digital communications by Gabor and it has always been natural to do so since then. However, it is often in-purposely skipped for convenience in presentation and/or in theoretical studies.
The two-dimensional signal Sn,k in Eq. (3) can be thought of as a two-dimensional sampling of the following short-time Fourier transform (STFT)
where {L-End}
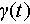 is called an analysis window in time domain. STFT is also called windowed Fourier transform. It was successfully applied in speech analysis in 1970s. Then, STFT was extensively studied in the era of wavelets of the 1990s as the first joint time-frequency analysis (JTFA) technique. Due to Gabor’s contribution, the two-dimensional sampling Sn,k in Eq. (3) of the STFT S(t,f) of signal s(t) in Eq. (4),
is called an analysis window in time domain. STFT is also called windowed Fourier transform. It was successfully applied in speech analysis in 1970s. Then, STFT was extensively studied in the era of wavelets of the 1990s as the first joint time-frequency analysis (JTFA) technique. Due to Gabor’s contribution, the two-dimensional sampling Sn,k in Eq. (3) of the STFT S(t,f) of signal s(t) in Eq. (4),
is called the Gabor transform of signal s(t) and the pulse p(t) in Eq. (3) is also called a synthesis window. The representation (3) is called Gabor representation (or expansion) of signal s(t). The pair (5) and (3) are called Gabor transform and representation pair. More on the sampling distances on times T and T′ and on frequencies W and W′ for Eqs. (3) and (5) to hold simultaneously was studied thoroughly by, for example, Daubechies in Ref. [2]. For finite length discrete time signals, they are called DGT and inverse DGT (IDGT) [3], respectively. Due to the best time and frequency localization property of Gaussian window function/pulse, Gabor transform and representation have important applications in signal analysis, see Ref. [4].
For the relationship between the synthesis and analysis window functions p(t) and γ(t) for Eqs. (3) and (5) to hold simultaneously either in continuous time or discrete time, Wexler and Raz [5] obtained an identity called Wexler-Raz identity in continuous time, discrete time, or finite length discrete time. The continuous time form of Wexler-Raz identity is
where T0 = 1/W and W0 = 1/T, and T′ = T and W′ = W in Eq. (5). Its discrete time versions are similar.
The relationship (6) corresponds to the biorthogonality of the analysis and synthesis windows γ(t) and p(t) that may not be the same and determine the forward and backward/inverse transforms, respectively. The design of these two window functions (or pulses) γ(t) and p(t) plays an important role not only in signal analysis but also in communications when signal s(t) is transmitted at transmitter and Sn,k needs to be detected at receiver.
In the oversampling case (for example, in the continuous time case, oversampling means TW < 1, and in the finite length discrete time signal case, oversampling means that the number of points in the DGT domain is more than the signal length in time domain), for a given synthesis window p(t), the analysis window γ(t) satisfying the Wexler-Raz identity (6) is not unique. The optimal γ(t) (called the most-orthogonal-like, i.e., {L-End}
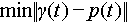 ) was proposed in Ref. [6] and obtained in Ref. [3] for finite length discrete time signals and in Ref. [7] for more generally linear transformed most-orthogonal-like set-up (i.e., {L-End}
) was proposed in Ref. [6] and obtained in Ref. [3] for finite length discrete time signals and in Ref. [7] for more generally linear transformed most-orthogonal-like set-up (i.e., {L-End}
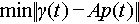 where A is any linear operator with a certain condition) in either discrete or continuous time.
where A is any linear operator with a certain condition) in either discrete or continuous time.
Interestingly, the generalized solution obtained in Ref. [7] is the same as the one without linear transformation, i.e., the same as that obtained in Ref. [3]. Also, interestingly, the optimal most-orthogonal-like solution coincides with the minimum norm solution in either discrete time Ref. [3] or continuous time Ref. [7], where these two solutions correspond to the two special cases of the above general optimization problem set-up in Ref. [7] when the linear operator A is the identity I and 0, respectively. For a finite discrete time, the DGT of a finite length signal of 1 dimension becomes a two-dimensional matrix. Its matrix rank was investigated and determined in Ref. [8].
A JTFA is for non-stationary signal analysis and usually concentrates a signal (such as a chirp signal) while spreading noise, which means that the signal-to-noise ratio (SNR) in a JTFA domain may be increased over that in time domain. A quantitative SNR analysis in a JTFA domain is given in Refs. [9−11], which basically says that the SNR in a JTFA domain of such a signal increases over the SNR in time domain or frequency domain linearly with the sampling rate in time domain of the signal. As we know that one important purpose of signal transformation is to clean a noisy signal, since the SNR may be increased in the transformation domain over that in time domain. Thus, it makes the cleaning easier in the joint time and frequency transformation domain than that in time domain or frequency domain alone.
When a signal is non-stationary or wideband, the traditional filtering in the Fourier domain may not work well, because the Fourier transform may not be able to concentrate the signal, i.e., the SNR in frequency domain may not increase much over that in time domain. In this case, one may apply a JTFA that may concentrate the signal while it spreads the noise, i.e., the SNR in a JTFA domain may be increased significantly over that in time domain or frequency domain as mentioned above. Thus, one may apply a filtering in the JTFA domain.
However, since a JTFA is usually not an onto transform, after the filtering/clean-up in the JTFA domain, the filtered two-dimensional signal may not correspond to a time domain signal, i.e., it may not be the JTFA of any time domain signal. Thus, filtering using JTFA (time-variant filtering) is not as trivial as that using the Fourier transform (time-invariant filtering). In this case, an iterative time-variant filter using DGT/IDGT is proposed in Ref. [12] with the convergence analysis. It says that the convergence is good for the most-orthogonal-like pair window functions. This DGT based time-variant filtering is used in system identification in low SNR environment in Ref. [13] by transmitting chirp signals, which may have applications in radar for target detection and in communications for channel estimation.
No transform can be universally good for every signal, including JTFA. In my opinion, JTFA works particularly well for chirp type signals, including high order chirps. A discrete chirp-Fourier transform (DCFT) is proposed in Ref. [14] for linear-chirp signal matching, where it shows that DCFT works optimally when the signal length is a prime number. Although fractional Fourier transform (FrFT) can also be used to match linear-chirp signals, the original motivation of FrFT is not about it and furthermore, it does not tell when it is optimal for a finite length discrete signal.
A good book on JTFA is Ref. [4] by Qian and Chen.
In this article, we have briefly recalled Gabor communication theory in the 1940s, which is from a different perspective of Shannon, and more from the physics and signal processing point of view, by packing signals in a time and frequency plane. In the later years, it has become Gabor atoms, Gabor transform, and Gabor expansion/representation for nonstationary signal analysis as a major JTFA tool.
Conflict of interest
The author declares no conflict of interest.
References
- Gabor D. Theory of communication. Part 1: The analysis of information. J Inst Electr Eng-Part III-Radio Commun Eng 1946; 93: 429-441. [Article] [Google Scholar]
- Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans Inform Theory 1990; 36: 961-1005. [Article] [Google Scholar]
- Qian S, Chen D. Discrete Gabor transform. IEEE Trans Signal Process 1993; 41: 2429-2438. [Article] [Google Scholar]
- Qian S, Chen D. Joint Time-Frequency Analysis: Methods and Applications. State of New Jersey: PTR Prentice Hall, 1996 [Google Scholar]
- Wexler J, Raz S. Discrete Gabor expansions. Signal Process 1990; 21: 207-221. [Article] [Google Scholar]
- Qian S, Chen K, Li S. Optimal biorthogonal functions for finite discrete-time Gabor expansion. Signal Process 1992; 27: 177-185. [Article] [Google Scholar]
- Xia XG. On characterization of the optimal biorthogonal window functions for Gabor transform. IEEE Trans Signal Process 1996; 44: 133-136. [Article] [Google Scholar]
- Xia XG, Qian S. On the rank of the discrete Gabor transform matrix. Signal Process 2001; 81: 1083-1087. [Article] [Google Scholar]
- Xia XG. A quantitative analysis of SNR in the short-time Fourier transform domain for multicomponent signals. IEEE Trans Signal Process 1998; 46: 200-203. [Article] [Google Scholar]
- Xia XG, Chen VC. A quantitative SNR analysis for the pseudo Wigner-Ville distribution. IEEE Trans Signal Process 1999; 47: 2891-2894. [Article] [Google Scholar]
- Xia XG, Wang GY, Chen VC. Quantitative SNR analysis for ISAR imaging using joint time-frequency analysis-short time Fourier transform. IEEE Trans Aerosp Electron Syst 2002; 38: 649-659. [Article] [Google Scholar]
- Xia XG, Qian S. Convergence of an iterative time-variant filtering based on discrete Gabor transform. IEEE Trans Signal Process 1999; 47: 2894-2899. [Article] [Google Scholar]
- Xia XG. System identification using chirp signals and time-variant filters in the joint time-frequency domain. IEEE Trans Signal Process 1997; 45: 2072-2084. [Article] [Google Scholar]
- Xia XG. Discrete chirp-Fourier transform and its application to chirp rate estimation. IEEE Trans Signal Process 2000; 48: 3122-3133. [Article] [Google Scholar]
© The Author(s) 2025. Published by Science Press and EDP Sciences.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.