| Issue |
Natl Sci Open
Volume 4, Number 5, 2025
|
|
|---|---|---|
| Article Number | 20250016 | |
| Number of page(s) | 20 | |
| Section | Information Sciences | |
| DOI | https://doi.org/10.1360/nso/20250016 | |
| Published online | 21 August 2025 | |
RESEARCH ARTICLE
Physics-informed neuromorphic learning: Enabling scalable industrial digital twins
1
School of Automation and Intelligent Sensing, Shanghai Jiao Tong University, Shanghai 200240, China
2
Key Laboratory for System Control and Information Processing, Ministry of Education, Shanghai 200240, China
3
Shanghai Key Laboratory for Perception and Control in Industrial Network Systems, Shanghai 200240, China
4
The Department of Electrical and Electronic Engineering, University of Manchester, Manchester M13 9PL, UK
5
SJTU-Paris Elite Institute of Technology, Shanghai Jiao Tong University, Shanghai 200240, China
6
Shanghai Key Laboratory of Integrated Administration Technologies for Information Security, Shanghai 200240, China
* Corresponding author (emails: cailianchen@sjtu.edu.cn (Cailian Chen); xpguan@sjtu.edu.cn (Xinping Guan))
Received:
24
April
2025
Revised:
8
July
2025
Accepted:
30
July
2025
Digital twins (DTs) have shown promise in industrial automation by facilitating seamless fusion between virtual and physical spaces, thereby enhancing operational efficiency. However, existing DTs are predominantly customized implementations, requiring advanced expertise and significant resources, which hinders their broader application. Here, we propose a physics-informed neuromorphic learning framework, a computationally efficient approach based on the brain-inspired structural representation. This physics-guided representation, inferred and integrated through prior cross-modal structural knowledge, provides a scalable foundation for DT construction with brain-like generalization capabilities and ultra-low computational complexity. We demonstrate its effectiveness across multiple industrial scenarios, attaining accuracy comparable to current DT modeling techniques while reducing computational latency to less than 1/30. This framework shifts the paradigm from complex, customized DTs to a simplified, unified solution, potentially saving considerable human and computational resources. By facilitating the practical integration of DTs into industrial workflows, our method marks a substantial advancement in accelerating industrial transformation.
Key words: industrial digital twin / industrial control system / machine learning
© The Author(s) 2025. Published by Science Press and EDP Sciences.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
INTRODUCTION
The digital twin (DT), a virtual representation of physical systems within a digital environment, is a transformative technology with wide-ranging implications. The importance of DTs has been recognized across multiple fields, with numerous studies highlighting their value [1-11]. In the realm of industry, by facilitating seamless fusion between virtual and physical spaces, DTs offer a powerful solution to optimize processes and guide the operations of industrial control systems (ICSs), thereby enhancing functionality, improving efficiency, and reducing costs [12, 13]. For instance, Boeing's implementation of DT technology has improved component and system quality by 40% in aircraft manufacturing, demonstrating its significant impact on product development and quality assurance [6]. Recognizing the significant potential for performance enhancement that DTs offer for industry, recent research has increasingly focused on advancing DT technologies for ICSs [14-19].
While these pioneering efforts have demonstrated clear advantages, their applicability to novel situations remains limited due to two key constraints: (1) the construction of an accurate mathematical model for a new ICS requires specialized expertise and is often impractical due to the inherent complexity of integrating cyber and physical components and their interdependencies; (2) a field-level ICS typically lacks in memory, computational power, and communication resources to support complex data-driven re-modeling in new contexts. Therefore, there is a growing demand for more context-independent and computational-efficient methodologies that move from one-off DTs to scalable DTs without compromising the fidelity of the digital representation.
A potential solution to address these challenges lies in leveraging the intelligence of the human brain, which excels at efficient information processing and generalizing past experiences to novel situations. This remarkable capability has garnered significant attention and inspired the development of artificial intelligence technologies, including feed-forward neural network [20], and convolutional neural network [21], among others. However, due to the incomplete understanding of the brain's underlying mechanisms, these neural networks only partially emulate cognitive processes, resulting in limited generalizability across diverse contexts. Furthermore, their reliance on multi-layer backpropagation for training necessitates significant computational resources, thereby restricting their applicability in industrial DT modeling.
A natural question is whether or not the DT modeling methods for ICSs can incorporate both the generalizability and efficiency inherent in the human brain. We noticed that one fundamental concept underpinning human cognitive capacity is the “cognitive map" [22-24], which is closely associated with brain structures such as the hippocampus and medial prefrontal cortex. The cognitive map functions as a mental representation that enables organisms to acquire, encode, store, retrieve, and decode information regarding the spatial and relational properties of objects and events in their environment [25, 26]. This capacity is grounded in the structured nature of the world, where new situations often share features with previously encountered ones. For instance, understanding the cause of the occurrence of sea breezes during the day, driven by spatial relationships and the logical relationships between specific heat capacity (SHC) contrast, temperature gradients, and pressure differentials, allows us to reasonably infer that land breezes arise at night due to similar mechanisms (Figure 1(a)). This suggests that structural representations may be a key preprocessing step in unlocking the full potential of human cognition [26], although the precise mechanisms of the entire biological cognitive loop remain unclear. Following these foundational insights into brain cognitive mechanisms, we seek to address two central questions in this paper: can DT modeling benefit from such structural knowledge? And, can the findings enhance our understanding of the entire biological cognitive loop that remain elusive from a biological perspective? Here, we propose a physics-informed neuromorphic learning (PINL) framework that conceptualizes DTs as “digital brains", drawing inspiration from the human brain's cognitive intelligence. This framework demonstrates the analogous role of structural representations of knowledge in cognitive mechanisms, both in biological and digital domains. To realize this analogy, the proposed dual-channel reservoir scheme—integrated within the inference infusion engine—leverages prior structural knowledge to infer and fuse cross-modal structural representations into a framework-embeddable structural code, enabling scalable DT construction with brain-like generalization capabilities and ultra-low computational complexity. The efficacy of PINL is validated across several representative ICS cases, including water treatment, power engineering, and the steel industry, among others. Results indicate that PINL successfully models the behavior of these complex dynamical systems and performs key guiding operations such as prediction, decision-making, and anomaly detection—all essential for realizing the full potential of DTs. Notably, the framework's performance aligns with two empirically recorded principles of biological cognition: (1) prior knowledge enhances cognition across environments, as observed in Ref. [25]; (2) structured knowledge facilitates inference and decision-making. These correspondences validate the role of the bio-inspired structural code in digital cognitive preprocessing. Furthermore, the interaction between the structural code and other framework components suggests a potential computational basis for the entire biological cognitive mechanism, revealing how the brain generates structural representations that can be generalized across diverse environments to facilitate specific cognitive tasks, thereby offering new insights into biological cognition. In addition to the capability of state-of-the-art approaches, the PINL introduces several unique features derived from its structural code-based foundation, extending beyond existing model-based and model-free DT modeling methods: (1) physics-informed: the structural code inherently encodes domain-specific physical laws, enabling PINL cross-scenario generalization in DT construction; (2) low expertise requirement: by automating the inference and fusion of cross-modal structural knowledge, PINL significantly reduces dependency on specialized modeling expertise; (3) optimally designed: the PINL generates the structural code through a systematic optimization process that balances between cross-modality consistency loss, model reconstruction loss, and model complexity, eliminating the need for manual tuning; (4) biologically grounded: by mirroring the brain's cognitive map mechanism through structural codes, the PINL framework enables a new class of digital transformation solutions with brain-like low complexity and minimal expert dependency; (5) cognitively interpretable: the incorporation of structural codes within the framework potentially offers a computational basis to investigate how structural knowledge supports downstream biological cognitive tasks, thereby establishing a link between digital and biological cognition.
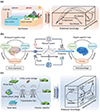 |
Figure 1 Cognitive processes in biological and digital spaces. (a) An example illustrating the human brain's remarkable ability to generalize past experiences to novel situations using structural knowledge (including spatial and relational knowledge). (b) Representation of the analogous closed-loop cognition in both biological and digital spaces. (c) Application of the proposed PINL to power grids, demonstrating the use of structural knowledge in a manner that mirrors biological cognitive processes. |
RESULTS
A common cognitive mechanism for digital and biological spaces
As shown in Figure 1(b), we propose the existence of a biological cognitive loop within the human brain that supports cognition and informs decision-making. This loop represents the fundamental process through which humans perceive, understand, and interact with the world, driven by neural activity. To learn from the environment, the brain first observes sensory information through various modalities, including visual, somatosensory, auditory, and entorhinal input. These sensory data are then encoded and transmitted to the hippocampus for memory storage and retrieval. During decision-making, the prefrontal cortex decodes both the current sensory input and the prior knowledge stored in the hippocampus, using this information to guide behavior. Our actions, in turn, influence the external environment. By iteratively implementing this process in our brain, we continuously refine our decision-making and optimize our responses to changing circumstances, ultimately leading to more effective and adaptive behavior over time.
Although this biological cognitive loop is first reported in this work, it is supported by numerous recent studies. Research indicates that both humans and other animals make complex inferences from limited observations, rapidly integrating new knowledge to guide behavior through a systematically organized knowledge structure known as a cognitive map. Electrophysiological research in rodents suggests that the hippocampus and the entorhinal cortex are the neurological basis of cognitive maps [23]. Specifically, the discovery of grid cells and place cells within these regions, particularly during spatial tasks, has shown that these areas organize information in a spatially structured manner [27]. Further evidence suggests that the brain utilizes cognitive maps to respond to both spatial and non-spatial tasks in a unified way [26]. These maps are also transformed across hippocampal-prefrontal networks, facilitating abstraction and generalization for memory-guided decision-making [25]. Building on these findings, we extract key concepts of the human cognitive process: perceiving the world, storing experiences, and controlling behavior.
Following the resembling pattern, we develop a digital cognitive loop that forms the core operational principle of DTs for ICSs. This process begins by continuously collecting data from sensors that monitor system states. The data are subsequently compressed and stored in a memory device, such as ROM. To guide system operations and provide subsequent instructions, the controller retrieves, decompresses, and analyzes both the current data and prior given principles. This closed-loop process enables the emulation of a digital brain capable of observing and controlling objects, thus guiding digital cognitive tasks.
To implement this digital cognitive loop, we develop the PINL framework. This framework mimics the cognitive intelligence of the human brain, enabling it to understand and modify the physical entity in question. For instance, as shown in Figure 1(c), structural knowledge of the smart grid—comprising both spatial and relational dimensions—is extracted to form the foundation to implement PINL. Spatial knowledge is derived from the topology of the smart grid, while relational knowledge pertains to the coordination of power supply and demand. If this proposed brain-like digitalization scheme is capable of serving as a foundation for scalable DT construction and unifying cognitive mechanisms in both biological and digital realms, three key predictions should be true. (1) The PINL should exhibit brain-like generalization capabilities across diverse industrial scenarios. (2) The PINL should exhibit experimental phenomena and conclusions similar to those observed in animals when processing cognitive tasks. (3) The PINL should possess low-complexity information processing and decision-making capabilities, comparable to those of the human brain. In the following sections, we will provide a detailed examination of the proposed PINL and assess these predictions.
Physics-informed neuromorphic learning framework
Based on the discovery of the digital cognitive loop, we propose the PINL as a virtual brain in digital space to facilitate the implementation of DTs, as shown in Figure 2. The PINL comprehends and controls industrial scenarios by utilizing encoded structural knowledge and acquired data. Specifically, the structural knowledge of an ICS comprises spatial knowledge AS and relational knowledge AR, outlining the topological connections and causal dependencies among variables, respectively. In practical industrial contexts, acquiring complete relational knowledge is often infeasible due to the complexity of physical and logical interactions. To address this, we propose an inference fusion engine (Figure 2(b))—the central component of the PINL framework—that empowers PINL to operate with incomplete prior knowledge. This engine infers a more comprehensive relational knowledge set from partial priors and integrates heterogeneous knowledge into an abstract structural code A by exploring the correlations among diverse structural representations. This mechanism parallels the function of the sensory cortex in the biological cognitive loop. By generating the structural code—a compact representation of the current environment within the learned structure—it facilitates efficient cross-modal inference and fusion, thereby establishing a foundation for scalable DT construction.
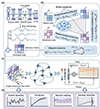 |
Figure 2 Schematic overview of the PINL for ICSs. (a) State monitoring for a simplified ICS, illustrated through a laminar cooling process. The steel temperature, the runout table speed, and the water flow rate are continuously monitored. (b) Inference fusion process for structural code generation. Spatial and relational prior knowledge, though potentially incomplete, is directly extracted from the ICS. The inference fusion engine infers more comprehensive structural knowledge by leveraging correlations between different knowledge patterns, balancing three goals: maintaining consistency between inferred spatial and relational knowledge, aligning inferred outputs with available prior knowledge, and avoiding overfitting. The resulting optimally established structural code represents the current environment within the learned structure, enabling generalization across diverse scenarios and providing a scalable foundation for DT construction. (c) Training process for graph-structured time series. The structural code convolves with the reservoir graph to simulate local cortical dynamics, facilitating rich representations of digital cognition. (d) Computational tasks within the digital cognitive loop. |
To derive the structural code 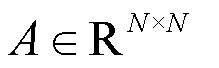 , we propose a dual-channel reservoir computing scheme, which serves as the core of the inference fusion engine, designed to integrate spatial and relational knowledge. Unlike conventional reservoir computing, which is designed for processing temporal data and focuses primarily on function approximation, the proposed scheme is tailored for unordered, non-temporal structural inputs. This design enables PINL to automate the inference and fusion of heterogeneous prior knowledge, thereby substantially reducing reliance on specialized modeling expertise. Furthermore, it generates the optimal structural code through a systematic optimization process that jointly balances cross-modality consistency, reconstruction fidelity, and model complexity. According to the aforementioned framework of PINL, we define the spatial graph
, we propose a dual-channel reservoir computing scheme, which serves as the core of the inference fusion engine, designed to integrate spatial and relational knowledge. Unlike conventional reservoir computing, which is designed for processing temporal data and focuses primarily on function approximation, the proposed scheme is tailored for unordered, non-temporal structural inputs. This design enables PINL to automate the inference and fusion of heterogeneous prior knowledge, thereby substantially reducing reliance on specialized modeling expertise. Furthermore, it generates the optimal structural code through a systematic optimization process that jointly balances cross-modality consistency, reconstruction fidelity, and model complexity. According to the aforementioned framework of PINL, we define the spatial graph 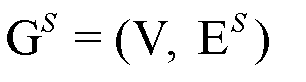 and relational graph
and relational graph 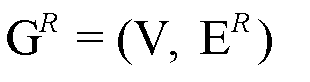 over
over 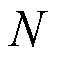 nodes, with corresponding adjacency matrices
nodes, with corresponding adjacency matrices 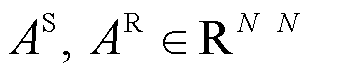 . These matrices encode binary-valued structural priors: ai,j = 1 if a link exists from node i to node j, and ai,j = 0 otherwise. Together, they form a structured knowledge space
. These matrices encode binary-valued structural priors: ai,j = 1 if a link exists from node i to node j, and ai,j = 0 otherwise. Together, they form a structured knowledge space 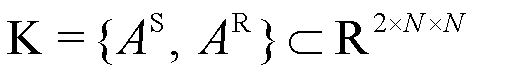 . The spatial matrix
. The spatial matrix 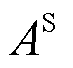 is symmetric and undirected, capturing physical connections, while the relational matrix
is symmetric and undirected, capturing physical connections, while the relational matrix 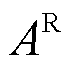 is asymmetric and directed, reflecting causal dependencies such that
is asymmetric and directed, reflecting causal dependencies such that 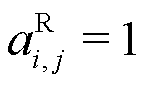 implies conditional dependence of node j on node i. To ensure structural self-consistency during the fusion process, a monotonic preservation constraint is introduced: for any node pairs (i, j) and (p, q),
implies conditional dependence of node j on node i. To ensure structural self-consistency during the fusion process, a monotonic preservation constraint is introduced: for any node pairs (i, j) and (p, q),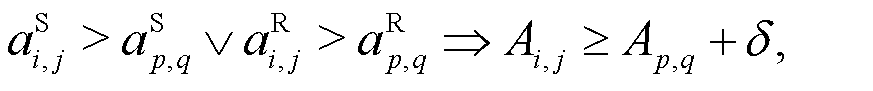 (1)where (δ > 0) is a margin hyperparameter. This constraint aligns the fused representation with domain-specific intuitions of structural representations.
(1)where (δ > 0) is a margin hyperparameter. This constraint aligns the fused representation with domain-specific intuitions of structural representations.
To compute the structural code A, we define a fusion operator 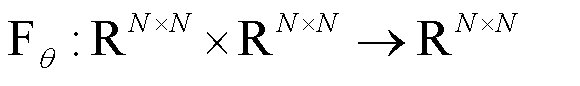 , parameterized by the internal dynamics of the dual-channel reservoir layer:
, parameterized by the internal dynamics of the dual-channel reservoir layer: 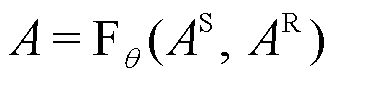 , where
, where 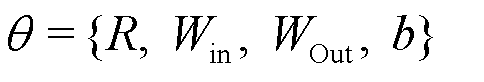 comprises the learnable and randomly initialized parameters. The evolving dual channel states r1(t+1) and r2(t+1) correspond to the spatial and relational inputs, respectively, which are updated iteratively using the following nonlinear updating procedure,
comprises the learnable and randomly initialized parameters. The evolving dual channel states r1(t+1) and r2(t+1) correspond to the spatial and relational inputs, respectively, which are updated iteratively using the following nonlinear updating procedure,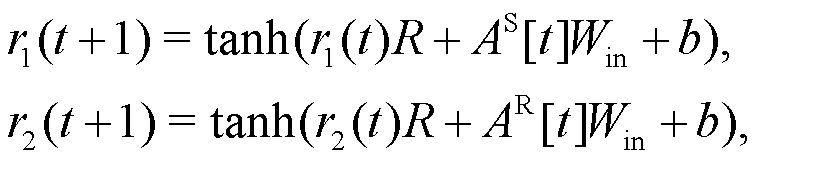 (2)where AS[t] and AR[t] denote the column vectors corresponding to spatial and relational inputs at time t, respectively. Here,
(2)where AS[t] and AR[t] denote the column vectors corresponding to spatial and relational inputs at time t, respectively. Here, 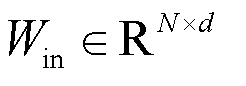 maps inputs into the reservoir space,
maps inputs into the reservoir space, 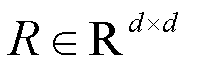 a sparse recurrent matrix (the reservoir graph) with spectral radius
a sparse recurrent matrix (the reservoir graph) with spectral radius 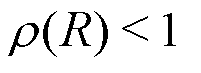 , and
, and 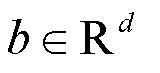 is a bias vector. The reservoir graph R defines the internal connectivity of the reservoir network, where each node (or vertex) corresponds to a neuron or processing unit within the reservoir and each edge represents the weighted connection between these neurons. These connections are typically sparse and initialized randomly. The encoded states
is a bias vector. The reservoir graph R defines the internal connectivity of the reservoir network, where each node (or vertex) corresponds to a neuron or processing unit within the reservoir and each edge represents the weighted connection between these neurons. These connections are typically sparse and initialized randomly. The encoded states 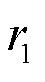 and
and 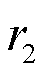 are then fused to form the structural code
are then fused to form the structural code 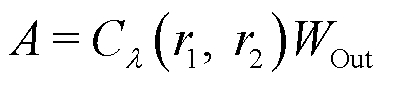 , where Cλ is the convex combination operator and
, where Cλ is the convex combination operator and 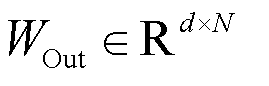 is a shared output projection matrix across modalities. The combination weight
is a shared output projection matrix across modalities. The combination weight 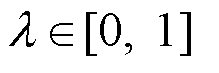 is computed as
is computed as 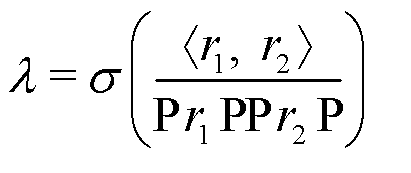 with σ denoting the sigmoid function. To promote cross-modality alignment and representational consistency, we introduce a cross-modality consistency loss
with σ denoting the sigmoid function. To promote cross-modality alignment and representational consistency, we introduce a cross-modality consistency loss 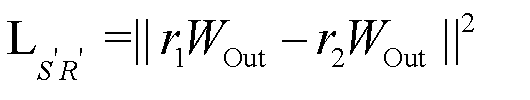 , which penalizes discrepancies between the two inferred structural forms. This formulation is grounded in the premise that spatially connected variables are more likely to be relationally correlated.
, which penalizes discrepancies between the two inferred structural forms. This formulation is grounded in the premise that spatially connected variables are more likely to be relationally correlated.
Furthermore, to ensure fidelity to prior knowledge, we introduce reconstruction losses 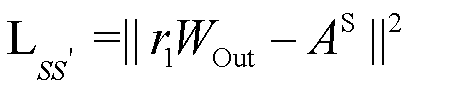 and
and 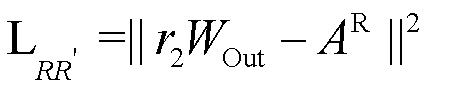 . To mitigate the risk of overfitting, we incorporate an L2 regularization term
. To mitigate the risk of overfitting, we incorporate an L2 regularization term 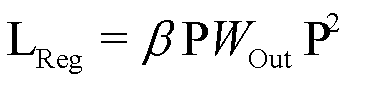 . The objective function (i.e., the mathematical expression of fusion operator
. The objective function (i.e., the mathematical expression of fusion operator 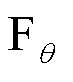 ) becomes a regularized optimization problem over the feasible space
) becomes a regularized optimization problem over the feasible space 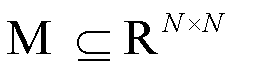 to determine the structural code
to determine the structural code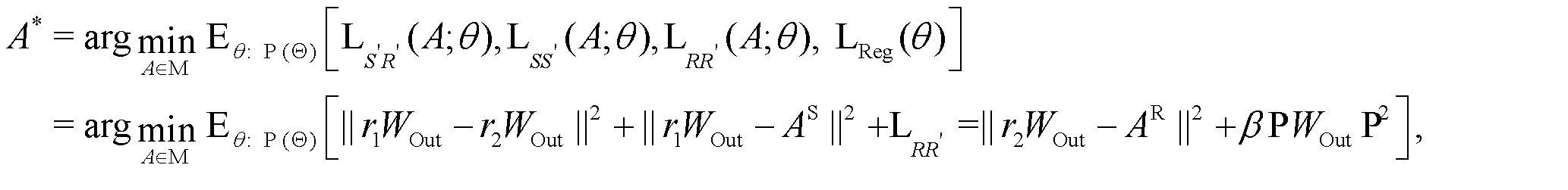 (3)where
(3)where 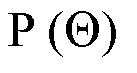 denotes a prior distribution over the functional parameters. This optimal formulation of the structural code bridges incomplete prior multi-modal knowledge with inferred correlations, maintaining generalization across diverse contexts, thereby addressing the scalability bottleneck in industrial DT construction. The optimal output projection matrix is given by
denotes a prior distribution over the functional parameters. This optimal formulation of the structural code bridges incomplete prior multi-modal knowledge with inferred correlations, maintaining generalization across diverse contexts, thereby addressing the scalability bottleneck in industrial DT construction. The optimal output projection matrix is given by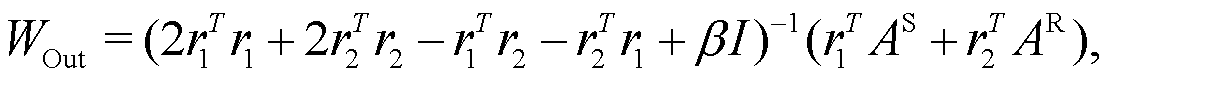 (4)with the detailed solution process provided in the section “Methods". To ensure that the constraint (1) is satisfied, we perform a post-check on the generated structural code after the calculation. Since the reservoir graph R is randomly generated, if the constraint is not satisfied, R is re-initialized and the optimization is repeated. This process ensures that the final structural code adheres to the monotonicity requirement.
(4)with the detailed solution process provided in the section “Methods". To ensure that the constraint (1) is satisfied, we perform a post-check on the generated structural code after the calculation. Since the reservoir graph R is randomly generated, if the constraint is not satisfied, R is re-initialized and the optimization is repeated. This process ensures that the final structural code adheres to the monotonicity requirement.
Finally, the fused structural code, when combined with real-time sensor data, produces a graph-structured time series for downstream processing (Figure 2(c)). The conventional reservoir layer, which reflects both the representational and dynamic characteristics observed in the prefrontal cortex [28], is utilized to perform downstream digital cognitive tasks. This is achieved by convolving the graph-structured time series with the reservoir graph. We have evaluated the performance of PINL by investigating four types of computational tasks within the digital cognitive loop: capturing system dynamics, predicting system status, making decisions, and detecting anomalies, all of which are essential to realizing the full potential of DTs.
Application to multiple scenarios
We first demonstrate the generalizability of our PINL in constructing DTs across different industrial applications. To this end, we apply the PINL to six distinct types of practical ICSs, including examples that range from nonlinear to high-dimensional systems. Figure 3 presents a summary of the testing results of PINL for the PINL applied to these diverse ICSs. For an in-depth analysis of these ICSs and the performance of the PINL, we refer the reader to Supplementary information Note 1, where a detailed exposition is provided.
 |
Figure 3 Overview of the testing outcomes for the PINL implemented across various ICSs. The PINL has been deployed across six representative ICSs. The y-axis is the time step, with each ICS having a distinct time step length based on its control accuracy requirements, while the x-axis represents the standardized values of variables in ICSs. (a) The prediction and anomaly detection capabilities of the PINL. The second and third columns display the predicted state variables from the digital space and the actual measured values from the ICSs, respectively. The fifth column is the calculated mean absolute percentage error (MAPE) for the prediction results. The final column reports the F1-score for anomaly detection, quantifying the DT's accuracy in distinguishing between normal and abnormal operational states. (b) The decision-making efficacy of the PINL. |
Linear ICS application—motor control system
This part explains the key concepts of PINL by examining a fundamental and widely used ICS: the speed control system for a brushless direct current (DC) motor. The objective of this ICS is to regulate the motors' angular velocity to a predetermined value by adjusting the supplied voltage. For illustration, we implement a simple feedback controller that ensures the motor adheres to the specified speed, utilizing a proportional-integral-derivative speed control strategy.
To establish a complete dataset, the state variables y(t) (including the current I, electromagnetic torque Te, and angular speed ω), the error e(t) that quantifies the deviation Δω between the desired and actual speeds, and the control instruction u(t) of the voltage value uv are sampled. To demonstrate the ability of PINL to detect abnormal conditions, an internal fault, along with three types of cyber attacks—namely, replay attacks, false data injection attacks, and denial of service attacks—are launched, as elaborated in Supplementary information Note 2. Both normal and abnormal data are collected for training and testing purposes. Following the construction process of structural code, the spatial code AS and relational code AR are founded based on the intuitive understanding of this application. For instance, the direct connection between the speed measurement sensor and the controller indicates a correlation between the variables uv and ω. The structure of AR is founded upon following fundamental observations that establish logical relationships among these variables,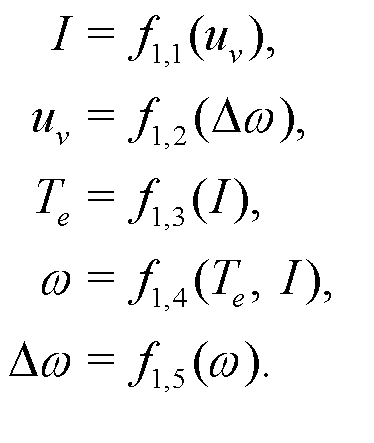 (5)
(5)
For example, electromagnetic torque Te is generated by the current I, while both Te and I influence the angular speed ω. Subsequently, these two adjacency matrices are forwarded to the inference fusion engine to form the structural code following the process in Figure 2(b). The obtained data, integrated with the prior structural knowledge, undergo processing following the training and testing procedure in Figure 2(c). The reservoir layer employed for digital cognitive task processing comprises 250 nodes, with a recurrent matrix spectral radius ρ(R)=0.8. The proposed PINL exhibits brain-like efficient information processing capability, with the training time for this scenario being a mere 0.427 s. Following this, we deploy the fine-tuned best DT in conjunction with this ICS for online testing. The testing process uses a sliding window method, with the time window length set to Tw=15. By monitoring every 15-step historical data sequence from the ICS, the PINL generates multiple graph slices for the next few time steps, which include predictions of sensor values (ω, I, Te), errors (Δω), and decision-making instructions for voltage adjustments (uv). These generated graphs are compared with the collected data from the ICS in the following time step to detect potential malfunctions or cyber intrusions through a threshold-based anomaly detection method.
Figure 4 illustrates the testing results of PINL when implemented in the motor speed control system. Under normal operating conditions, a minor discrepancy between the blue and orange lines signifies a strong level of agreement between the DT and the ICS, demonstrating that the proposed PINL effectively predicts sensor values and makes precise decisions. In contrast, under abnormal conditions, the divergence between the blue and orange lines serves as a criterion for identifying anomalies. An internal fault happens at the 50th time step, which is detected by the PINL 7 steps later. The last three columns demonstrate the PINL's efficacy in detecting cyber attacks. In each epoch, an attack initiates at the 100th time step and lasts for 50 time steps. The PINL successfully identifies these three attacks after 1, 3, and 4 time steps, respectively.
 |
Figure 4 The performance of PINL in the context of motor speed control system. The blue line represents the predictions and inferences generated by PINL, while the orange line reflects the data collected from the ICS. The time step is set to 0.05 s, aligning the controller's sampling rate with this interval. The first column displays normal conditions in the absence of any internal faults or external intrusions. The second column depicts a scenario where a fault in the speed sensor results in a deviation from the actual value. The remaining three columns verify the performance of PINL under cyber attacks. |
In summary, PINL successfully captures the dynamics of the motor speed control system, including both the intrinsic law of the physical process and the controller's strategy. While this is a simple system, as will be demonstrated in the following part, the PINL remains effective in multiple representative ICSs from various industrial sectors that exhibit more complex dynamics.
Multi-objective ICS application—power system
This example delineates the application of the proposed PINL to a typical scenario within power system operations, specifically the combined load frequency control and automatic voltage regulation [29]. This ICS is critical for the maintenance of stable frequency and voltage levels within the smart grid, as any deterioration in these two parameters can seriously compromise power quality. In contrast to the more straightforward case of motor speed control, this ICS involves multiple inputs and outputs, thereby necessitating the simultaneous adjustment of both voltage and frequency. PINL operates in conjunction with the ICS, continuously monitoring its states, providing predicted sensor values, and instructing corresponding decisions. The reservoir layer for digital cognitive task processing comprises 50 nodes, with a recurrent matrix spectral radius ρ(R)=0.7. The results show that PINL effectively captures the dynamics of this ICS, particularly demonstrating high accuracy in inferring decisions regarding frequency and voltage regulation, as illustrated in Figure 4. It also demonstrates a high capability for recognizing faults and external intrusions, achieving an F1-score of 98.86%. The mean absolute percentage error (MAPE) for predictions is 1.08%, while the MAPE for decision-making is 1.05%. This application demonstrates the efficacy of PINL in capturing complex dynamics of industrial applications characterized by multiple objectives.
Nonlinear ICS application—steel industry
In this example, we apply the PINL to a typical ICS in the steel industry, i.e., laminar cooling [30]. This process involves the application of laminar flow water to cool a hot steel strip. This cooling process not only enhances productivity but also significantly contributes to grain refinement and the enhancement of mechanical properties. The laminar cooling process exhibits intricate nonlinear features due to the consideration of heat transfer and exchange dynamics, including radiation, convection through air and water, conduction with the roller, and the latent heat associated with phase transformations. The laminar cooling process mainly consists of a pyrometer, a velocimeter, run-out table motors, and spray header equipment. The objective of this process is to effectively reduce the temperature of strip steel from an initial range of approximately 700 °C–900 °C to a final range of about 500 °C–700 °C. This temperature reduction is achieved by regulating the run-out table's speed and the sprayed water volume. The reservoir layer for digital cognitive task processing comprises 200 nodes, with a recurrent matrix spectral radius ρ(R)=0.8. Following data collection from this ICS, the PINL successfully captures the system dynamics through continuous monitoring, enabling accurate predictions and informed decision-making. The MAPE for predictions is 0.83%, while for decision-making, it is 0.82%. Additionally, the PINL successfully identifies faults and external intrusions, achieving an F1-score of 97.67%. Detailed testing results are presented in Supplementary information Figure S4. This application exemplifies the capabilities of PINL in revealing the underlying mechanistic models of complex nonlinear industrial applications that contain multiple control variables.
High-dimensional ICS application—water treatment
This example presents the case when applying PINL to a typical scenario in water treatment, i.e., the activated sludge process. The objective of this ICS is to regulate the dissolved oxygen concentration in the water. This regulation is crucial for fostering the growth of biological organisms that are essential for the degradation of organic carbon substances present in sewage. The reservoir layer for digital cognitive task processing comprises 600 nodes, with a recurrent matrix spectral radius ρ(R)=0.7. In addition to precise monitoring and synchronization with physical systems, PINL correctly detects the deviation from a normal condition, including sensor malfunctions and three kinds of cyber attacks, achieving an F1-score of 95.37%. Detailed testing results can be found in Supplementary information Figure S5, while the robustness of PINL against minor noise disturbances is discussed in Supplementary information Note 4. This example focuses on a nonlinear biological process with four dimensions, thereby illustrating the capabilities of PINL in managing nonlinear, high-dimensional industrial processes.
ICS with a different control strategy—chemical industry
In this example, we apply the PINL to a typical ICS in the chemical industry, i.e., a continuously stirred tank reactor (CSTR). The goal of the CSTR considered in this work is to simulate the isothermal series/parallel Van de Vusse reaction [31] using both a concentration sensor and a valve actuator. This ICS facilitates the catalytic oxidation of ethylene to acetic acid, utilizing molecular oxygen as the oxidant. The simulation focuses on controlling the feed flow to achieve the desired product concentration. Different from the above applications, this ICS is managed by a two-degree-of-freedom proportional-integral-derivative controller. The reservoir layer for digital cognitive task processing comprises 300 nodes, with a recurrent matrix spectral radius ρ(R)=0.5. The PINL effectively imitates and guides this ICS, achieving a MAPE of 0.16% in predictive accuracy and 0.34% in decision-making processes. Moreover, the F1-score in detecting the abnormality is 90.0% in this case. This example highlights the non-linear dynamics of the chemical reaction process, showcasing the capabilities of PINL to capture the dynamics of the ICS using various control strategies.
ICS with imprecise prior structural knowledge—renewable energy
This example illustrates the application of the proposed PINL in a typical scenario within the renewable energy industry, specifically in wind turbine energy conversion, where accurate structural knowledge is unavailable. In contrast to the ICS previously discussed, we utilized real data collected from anomalous wind turbines in large wind farms, as reported in Ref. [32]. Due to business confidentiality, the authors have not disclosed the technical details of the turbines; therefore, the structural code is inferred based on our foundational understanding of the wind energy conversion process. The data were collected over a period of 12–24 months with a 10-min sampling interval. Overall, 10 features were collected, including environmental temperature, wind speed, hub speed, and generator-side active power. The reservoir layer for digital cognitive task processing comprises 600 nodes, with a recurrent matrix spectral radius ρ(R)=0.7.
Despite limited insights into the specifics of the anomalous wind turbine, the proposed PINL demonstrates a relatively low prediction error for system states and achieves an F1-score of 76.6% in anomaly detection in the initial test. This highlights the validity and generalizability of the proposed PINL, even in the presence of imprecise prior structural knowledge, akin to the brain's reduced cognitive ability when relying on fuzzy experiences. However, the performance in this scenario is outperformed by its application to the other five scenarios. A key reason for this was a notable discrepancy between the PINL output and the ICS output for one critical decision variable—power generation. This discrepancy undermined the effectiveness of power planning supplied to the grid, primarily because power generation is strongly correlated with wind speed, which exhibits rapid fluctuations. As a result, the MAPE for power generation and planned power supply exceeded 25%. By contrast, PINL performed much better for variables with slower dynamics, such as environmental temperature. To validate the impact of variable change rates, we conducted further experiments excluding power generation and planned power supply from the dataset. The results showed substantial improvement: the prediction and decision errors dropped to 1.79% and 5.89%, respectively, and the F1-score for anomaly detection increased to 90.53%, as detailed in Supplementary information Figure S7. These findings indicate that the coarse temporal resolution (with a time step of 10 min in this case) failed to capture the fast dynamics of variables like wind power generation, leading to large prediction and decision errors. However, this resolution was sufficient for variables with slower dynamics. This confirms that a low sampling frequency might amplify the volatility of fast-changing variables, impeding PINL's ability to capture their nonlinear relationships effectively. Based on these findings, it is advisable to collect data at a high sampling frequency to promote the accuracy of PINL. In practical applications, acquiring sufficient data at shorter time intervals is typically feasible and does not pose a considerable challenge.
The promoting effect of prior structural knowledge on PINL
It has been observed that prior knowledge enhances learning in novel environments, particularly in spatial memory tasks that involve hippocampal-prefrontal interactions in rats [25]. If the proposed PINL offers a model for understanding the biological cognitive loop, it is expected to exhibit similar phenomena. To assess the influence of prior structural knowledge on the PINL's performance, we conducted a comparative analysis across the aforementioned applications. The aim of this evaluation is to determine whether the incorporation of prior structural knowledge improves the efficacy of the PINL, as illustrated in Figure 5(a)–(c). In the absence of prior knowledge, the structural code is randomly generated to initialize the graph's structure. After this initialization, the remaining procedures follow the standard PINL scheme.
 |
Figure 5 Evaluation of PINL's performance. (a)–(c) Effects of the integration of the structural knowledge on the performance of PINL. When no prior knowledge is available, i.e., model-free digital twin (MFDT), the structural code A is randomly generated to construct the graph skeleton. (d) Effects of network size on training time obtained from 20 trails across various ICSs. (e)–(h) Comparisons with representative machine learning-based DTs. (e)–(g) Accuracy comparison in prediction, decision-making, and anomaly detection. The proposed PINL scheme achieves comparable accuracy in capturing system dynamics and control policies in contrast to FNN-DT and STGNN-DT. (h) Model training time. A longer training time indicates greater computational demands and a lengthy testing process for parameter adjustments. Notably, the PINL has the least training time, underscoring its potential for practical implementation in ICSs with minimal effort. |
Overall, the integration of structural knowledge (spatial and relational knowledge) with data promotes the PINL's capability to identify the abnormality while achieving almost the same MAPE of prediction and decision-making compared with the condition when prior structural knowledge is absent. This provides evidence of alignment of the proposed digital and biological cognitive loop.
When only limited structural knowledge is available, the PINL functions analogously to the brain, inferring missing information based on previously acquired structural knowledge, as further detailed in Supplementary information Note 3. The results show that the PINL performs better when equipped with global knowledge than partial knowledge, mirroring the cognitive process in the biological brain where access to global information facilitates more rational decision-making than reliance on local information.
Evaluation of computational complexity and performance
In this section, we first present the computational complexity of our proposed PINL method and then compare its average construction and implementation time with model-based and learning-based DTs, namely MDT and STGNN-DT.
The training time for all six industrial applications is first recorded to illustrate the low training effort required by PINL. The computational burden for developing PINL mainly comes from two parts: (1) structural code generation; (2) digital cognitive task training. Our proposed dual-channel reservoir computing scheme generates structural codes by simultaneously processing spatial and relational knowledge through solving Equation (4), which involves simple, low-dimensional matrix operations. This design not only keeps the computational burden of structural code generation low but also enables our PINL cross-modal knowledge fusion, physics-informed modeling, and reduced reliance on domain expertise. The main computational load arises from the conventional reservoir computing used for digital cognitive tasks, lying in the training of the single output layer, with theoretical training time being linearly proportional to the reservoir size. Experiment results, including maximum, minimum, and average training time from 20 independent trials, are presented in Figure 5(d). For all examined ICSs, the maximum training time for the corresponding PINL is approximately 20 s, indicating the feasibility of rapid implementation in practical ICSs. The findings indicate that a deeper or wider network requires more training effort, consequently leading to increased computational time. These experimental results align with the theoretical analysis of computational complexity.
MDT is developed manually, following the manual process outlined in Ref. [33], whereas STGNN-DT utilizes a state-of-the-art machine learning technique (spatial-temporal graph neural network) [34] to effectively capture complex spatial-temporal dependencies among variables. The results are shown in Table 1, with the first column estimating the time required for MDT generation. To perform a fair comparison, we ensure identical experimental conditions for STGNN-DT and PINL, including the same inputs and training epochs. It is shown that the creation of an MDT is a labor-intensive process, necessitating expert analysis to explore the underlying principles of each custom implementation for one-off DT development. Although STGNN-DT requires less time for model construction compared with MDT, its training and the corresponding parameter adjustment processes are time-consuming and resource-intensive. In contrast, our proposed PINL enables rapid development and deployment, completing the process within tens of minutes, thereby conserving substantial human and computational resources.
Comparison of average time consumption to generate and deploy the digital twina)
We also evaluate the effectiveness of the classical feed-forward neural network (FNN) and the state-of-the-art spatial-temporal graph neural network (STGNN) [34] as alternatives to the proposed PINL to construct DTs, namely FNN-DT, STGNN-DT. The comparison results, shown in Figure 5(e)–(h), indicate that the PINL exhibits significantly lower computational complexity, reducing computational latency by more than 30 times compared to DT with alternative machine learning architectures, while achieving nearly equivalent accuracy in prediction, decision-making, and anomaly detection. These findings suggest that the proposed PINL possesses efficient information processing and decision-making capabilities similar to those of the brain, accelerating the DT modeling process without compromising the fidelity of the digital representation.
DISCUSSION
In summary, we have presented a novel method for constructing DTs for ICSs that possesses brain-like generalization and ultra-low computational complexity. This approach is established based on the discovery that structural knowledge, comprising spatial and relational components, and plays a similar role in cognitive mechanisms in both biological and digital domains. The proposed inference fusion engine, integrated within the PINL, enables not only the inference of unknown relational knowledge but also the fusion of different knowledge types into an abstract structural code that facilitates data integration. Consequently, the PINL successfully replicates key advantages of the human brain's generalizability and information processing efficiency when processing digital cognitive tasks within the DT, including prediction, decision-making, and anomaly detection. Additionally, the PINL is adaptable to scenarios where structural knowledge is entirely absent or only partially available, as detailed in Supplementary information Note 3. The performance of the proposed PINL aligns with empirically recorded principles in the biological cognition process from two aspects. First, the integration of structural knowledge (spatial and relational knowledge) with data promotes the PINL's cognitive capabilities, mirroring findings from animal studies that prior knowledge supports learning in novel environments. Second, when encountering scenarios, both the PINL and the human brain can infer possible knowledge to serve as a foundation for decision-making based on existing structural knowledge. This correspondence offers valuable insights into the brain's cognitive mechanisms, highlighting how prior knowledge is utilized to form flexible representations that generalize across diverse environments, thereby advancing our understanding of both digital and biological cognition.
The advantages of PINL have been experimentally validated across a range of ICSs, including laminar cooling in the steel industry, co-regulation of load frequency and voltage in the power system, activated sludge process in water treatment, CSTR in the chemical industry, and wind turbine in renewable energy. These representative applications cover diverse features of different ICSs, such as non-linearity, multivariable, high dimensionality, and varying control strategies. We have seen that PINL achieves precise prediction and decision-making, with the MAPE all below 6%. Moreover, PINL effectively identifies anomalous conditions, including device malfunctions and external intrusions, achieving an F1-score exceeding 90% across all the presented six applications. By unifying system cognitive mechanisms in biological and digital spaces, our work provides a new class of digital transformation solutions featured with remarkably low computational complexity and high generalizability, which has the potential to save hundreds of hours of human and computational effort, thereby facilitating its applicability to complex real-world ICSs.
While the proposed PINL presents several advantages, there are still some open questions to address in the future. The biological analogy in our work serves primarily as an intuitive conceptual aid rather than a precise emulation of biological processes, which inevitably involves some simplification. The PINL is inspired by key principles of biological cognition, particularly the role of structural knowledge in supporting flexible and efficient cognitive functions. This analogy has been instrumental in guiding the design of PINL, enabling it to capture essential features that enhance the scalability of DTs. However, important differences remain: biological cognition has evolved over millions of years and exhibits a level of complexity and adaptability that far exceeds our engineered model. Our approach is optimized for the efficiency and generalizability of DT applications rather than full biological fidelity. Future work may incorporate more detailed biological evidence to further refine and extend the model, moving toward a more comprehensive emulation of biological cognitive mechanisms and advanced digital cognition. Moreover, conventional control algorithms are implemented into a hardware-based programmable logic controller, which functions as the central component of an ICS, responsible for calculating decision-making instructions. In this work, the current processes and dynamics of ICSs in Applications 1–5 (in Supplementary information) have been established utilizing the open-source software OpenPLC [35] rather than through a hardware-based physical system. OpenPLC provides a software-based environment that replicates the behavior and functionalities of hardware programmable logic controllers (PLCs). The capabilities of this software are deemed equivalent to those of a hardware programmable logic controller, as it can execute programs originally designed for hardware PLCs without modification. This compatibility stems from OpenPLC's compliance with the IEC 61131-3 standard—the international standard for PLC programming languages—which defines the structure and syntax for programming industrial controllers. As a result, programs written in languages such as ladder diagram, or structured text can be seamlessly implemented both in OpenPLC and on actual hardware PLCs. It is noteworthy that the construction of PINL does not rely on an accurate model of the physical process, and it is evident that PINL has the capability to capture the dynamics using a real dataset, as shown in Application 6 (in Supplementary information). Thus, it is reasonable to consider extending the use of PINL to hardware contexts, provided that a sufficient volume of data is accessible. A final aspect is that the current version of PINL is inapplicable to the scenario where the system model and coefficients vary. For example, if new devices are introduced or existing ones are replaced with alternatives that possess different dynamic features, then the original PINL may exhibit diminished performance. Fortunately, this limitation can be mitigated through retraining the PINL, as it only requires little time to retrain the reservoir due to its low computing complexity. Following a short retraining period, the PINL can be updated to accommodate the new conditions.
METHODS
System setups
We conducted the experiments on a laptop equipped with a 3.10 GHz CPU (AMD Ryzen 7 5800H) and 16 GB of RAM, without reliance on a GPU. All implementations were developed in Python 3.7 using the PyTorch framework. For the dual-channel reservoir computing scheme (as illustrated in Figure 2(b)), the reservoir graph size was set to 10 and the bias vector b = 0.8. The sparse recurrent matrix R was randomly generated to satisfy a spectral radius constraint of ρ(R) = 0.8. The initial values of r1 and r2 were set to zero. For the conventional reservoir computing layer (as shown in Figure 2(c)), the reservoir graph size varied from 200 to 600 (adjusted and fine-tuned for each scenario), with the spectral radius ranging from 0.5 to 0.8, and the bias vector b = 0.8. The reservoir state was initially set to zero. Supplementary information Table S10 provides details of the datasets used in the experiments.
The optimal structural code
To enable the formulation of optimal structural code, the output weight matrix 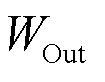 is learned by minimizing the objective function specified in Equation (3). This optimization balances three critical goals: maintaining consistency between inferred spatial and relational knowledge, aligning inferred outputs with available prior knowledge, and avoiding overfitting through regularization.
is learned by minimizing the objective function specified in Equation (3). This optimization balances three critical goals: maintaining consistency between inferred spatial and relational knowledge, aligning inferred outputs with available prior knowledge, and avoiding overfitting through regularization.
Formally, the optimal solution is obtained via the minimization of the loss function (3). The total loss 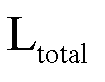 expands to
expands to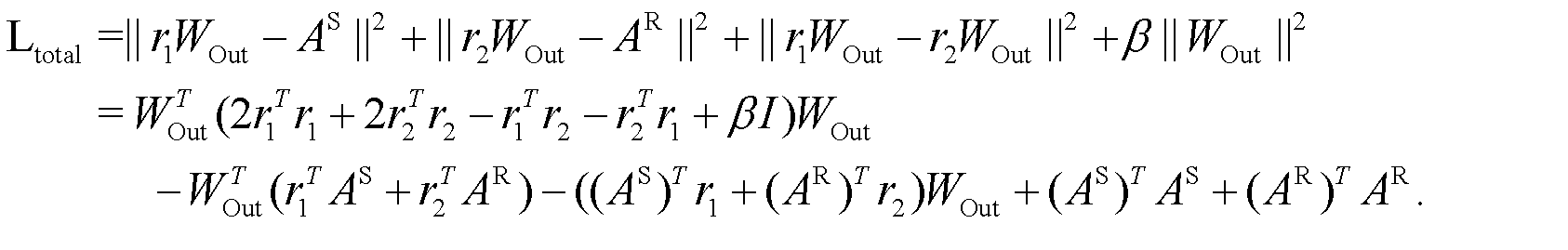 (6)
(6)
Taking the derivative with respect to 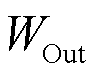 and setting it to zero yields:
and setting it to zero yields: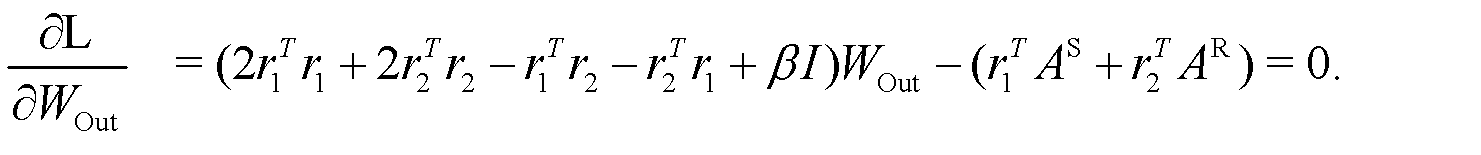 (7)
(7)
Solving this equation leads to the optimal output: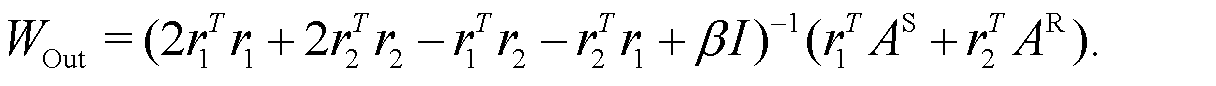 (8)
(8)
This optimization directly supports the functionality of the inference fusion engine, ensuring that the fused structural code 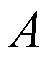 preserves both prior knowledge and inferred relations. The analytical solution's low computational complexity ensures its generalization performance across diverse industrial contexts, thereby guaranteeing the scalability of PINL.
preserves both prior knowledge and inferred relations. The analytical solution's low computational complexity ensures its generalization performance across diverse industrial contexts, thereby guaranteeing the scalability of PINL.
Performance metrics
The common performance metrics MAPE and F1-score are used for performance assessment,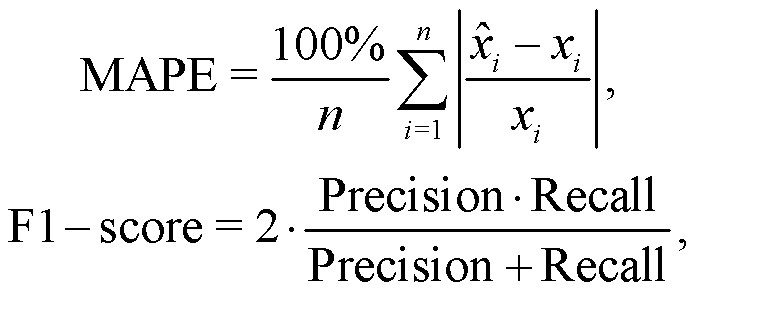 (9)where “Precision" and “Recall" are defined as
(9)where “Precision" and “Recall" are defined as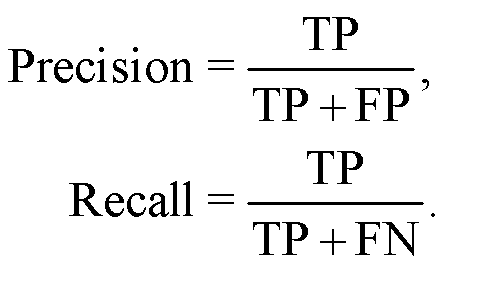 (10)
(10)
In Equation (10), TP, TN, and FN denote the number of true positive, true negative, and false negative samples, respectively.
Funding
This work was supported by the National Natural Science Foundation of China (62432009, 92167205, 624B2093, and U22A2050).
Author contributions
X.L., C.C. and Q.X. procured funding. X.G., C.C., Q.S. and Q.X. directed research. X.L. performed the research and wrote the paper. Y.T. contributed to visualization. L.X., Y.Z., Z.D. and Q.S. reviewed and edited the paper.
Conflict of interest
The authors declare no conflict of interest.
Supplementary information
Supplementary file provided by the authors. Access here
References
- Jin T, Sun Z, Li L, et al. Triboelectric nanogenerator sensors for soft robotics aiming at digital twin applications. Nat Commun 2020; 11: 5381.[Article] [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Coorey G, Figtree GA, Fletcher DF, et al. The health digital twin: Advancing precision cardiovascular medicine. Nat Rev Cardiol 2021; 18: 803–804.[Article] [Google Scholar]
- Maksymenko K, Clarke AK, Mendez Guerra I, et al. A myoelectric digital twin for fast and realistic modelling in deep learning. Nat Commun 2023; 14: 1600.[Article] [Google Scholar]
- Kim S, Heo S. An agricultural digital twin for mandarins demonstrates the potential for individualized agriculture. Nat Commun 2024; 15: 1561.[Article] [Google Scholar]
- White G, Zink A, Codecá L, et al. A digital twin smart city for citizen feedback. Cities 2021; 110: 103064.[Article] [Google Scholar]
- Mendi AF, Erol T, Dogan D. Digital twin in the military field. IEEE Internet Comput 2022; 26: 33–40.[Article] [Google Scholar]
- Kannan K, Arunachalam N. A digital twin for grinding wheel: An information sharing platform for sustainable grinding process. J Manuf Sci Eng 2019; 141: 021015.[Article] [Google Scholar]
- Batty M. Digital twins in city planning. Nat Comput Sci 2024; 4: 192–199.[Article] [Google Scholar]
- Bauer P, Stevens B, Hazeleger W. A digital twin of Earth for the green transition. Nat Clim Chang 2021; 11: 80–83.[Article] [Google Scholar]
- Li X, Feng M, Ran Y, et al. Big Data in Earth system science and progress towards a digital twin. Nat Rev Earth Environ 2023; 4: 319–332.[Article] [Google Scholar]
- Sizemore N, Oliphant K, Zheng R, et al. A digital twin of the infant microbiome to predict neurodevelopmental deficits. Sci Adv 2024; 10: eadj0400.[Article] [Google Scholar]
- Tao F, Zhang H, Zhang C. Advancements and challenges of digital twins in industry. Nat Comput Sci 2024; 4: 169–177.[Article] [Google Scholar]
- Tao F, Qi Q. Make more digital twins. Nature 2019; 573: 490–491.[Article] [CrossRef] [Google Scholar]
- Lei Z, Zhou H, Dai X, et al. Digital twin based monitoring and control for DC-DC converters. Nat Commun 2023; 14: 5604.[Article] [Google Scholar]
- Wei Y, Hu T, Zhou T, et al. Consistency retention method for CNC machine tool digital twin model. J Manuf Syst 2021; 58: 313–322.[Article] [Google Scholar]
- Lv Z, Xie S. Artificial intelligence in the digital twins: State of the art, challenges, and future research topics. Digital Twin 2022; 1: 12.[Article] [Google Scholar]
- Kapteyn MG, Pretorius JVR, Willcox KE. A probabilistic graphical model foundation for enabling predictive digital twins at scale. Nat Comput Sci 2021; 1: 337–347.[Article] [Google Scholar]
- Hürkamp A, Gellrich S, Ossowski T, et al. Combining simulation and machine learning as digital twin for the manufacturing of overmolded thermoplastic composites. J Manuf Mater Process 2020; 4: 92.[Article] [Google Scholar]
- Gehrmann C, Gunnarsson M. A digital twin based industrial automation and control system security architecture. IEEE Trans Ind Inf 2020; 16: 669–680.[Article] [Google Scholar]
- Bebis G, Georgiopoulos M. Feed-forward neural networks. IEEE Potentials 1994; 13: 27–31.[Article] [CrossRef] [Google Scholar]
- Li Z, Liu F, Yang W, et al. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans Neural Netw Learn Syst 2022; 33: 6999–7019.[Article] [Google Scholar]
- Tolman EC. Cognitive maps in rats and men. Psychol Rev 1948; 55: 189–208.[Article] [Google Scholar]
- Epstein RA, Patai EZ, Julian JB, et al. The cognitive map in humans: Spatial navigation and beyond. Nat Neurosci 2017; 20: 1504–1513.[Article] [Google Scholar]
- Bellmund JLS, Gärdenfors P, Moser EI, et al. Navigating cognition: Spatial codes for human thinking. Science 2018; 362: eaat6766.[Article] [Google Scholar]
- Tang W, Shin JD, Jadhav SP. Geometric transformation of cognitive maps for generalization across hippocampal-prefrontal circuits. Cell Rep 2023; 42: 112246.[Article] [Google Scholar]
- Whittington JCR, Muller TH, Mark S, et al. The tolman-eichenbaum machine: Unifying space and relational memory through generalization in the hippocampal formation. Cell 2020; 183: 1249–1263.e23.[Article] [Google Scholar]
- Moser EI, Kropff E, Moser MB. Place cells, grid cells, and the brain's spatial representation system. Annu Rev Neurosci 2008; 31: 69–89.[Article] [Google Scholar]
- Enel P, Procyk E, Quilodran R, et al. Reservoir computing properties of neural dynamics in prefrontal cortex. PLoS Comput Biol 2016; 12: e1004967.[Article] [Google Scholar]
- Saadat H. Power System Analysis. New York: WCB/McGraw-Hill, 1999. [Google Scholar]
- Li H, Li Z, Yuan G, et al. Development of new generation cooling control system after rolling in hot rolled strip based on UFC. J Iron Steel Res Int 2013; 20: 29–34.[Article] [Google Scholar]
- van de Vusse JG. A new model for the stirred tank reactor. Chem Eng Sci 1962; 17: 507–521.[Article] [Google Scholar]
- Zhan J, Wang S, Ma X, et al. STGAT-MAD: Spatial-temporal graph attention network for multivariate time series anomaly detection. In: Proceedings of the 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Singapore, 2022, 3568–3572. [Google Scholar]
- Ren C, Chen C, Li P, et al. Digital-twin-enabled task scheduling for state monitoring in aircraft testing process. IEEE Internet Things J 2024; 11: 26751–26765.[Article] [Google Scholar]
- Zheng Y, Koh HY, Jin M, et al. Correlation-aware spatial-temporal graph learning for multivariate time-series anomaly detection. IEEE Trans Neural Netw Learn Syst 2024; 35: 11802–11816.[Article] [Google Scholar]
- Alves T, Morris T. OpenPLC: An IEC 61,131-3 compliant open source industrial controller for cyber security research. Comput Security 2018; 78: 364–379.[Article] [Google Scholar]
All Tables
All Figures
 |
Figure 1 Cognitive processes in biological and digital spaces. (a) An example illustrating the human brain's remarkable ability to generalize past experiences to novel situations using structural knowledge (including spatial and relational knowledge). (b) Representation of the analogous closed-loop cognition in both biological and digital spaces. (c) Application of the proposed PINL to power grids, demonstrating the use of structural knowledge in a manner that mirrors biological cognitive processes. |
| In the text | |
 |
Figure 2 Schematic overview of the PINL for ICSs. (a) State monitoring for a simplified ICS, illustrated through a laminar cooling process. The steel temperature, the runout table speed, and the water flow rate are continuously monitored. (b) Inference fusion process for structural code generation. Spatial and relational prior knowledge, though potentially incomplete, is directly extracted from the ICS. The inference fusion engine infers more comprehensive structural knowledge by leveraging correlations between different knowledge patterns, balancing three goals: maintaining consistency between inferred spatial and relational knowledge, aligning inferred outputs with available prior knowledge, and avoiding overfitting. The resulting optimally established structural code represents the current environment within the learned structure, enabling generalization across diverse scenarios and providing a scalable foundation for DT construction. (c) Training process for graph-structured time series. The structural code convolves with the reservoir graph to simulate local cortical dynamics, facilitating rich representations of digital cognition. (d) Computational tasks within the digital cognitive loop. |
| In the text | |
 |
Figure 3 Overview of the testing outcomes for the PINL implemented across various ICSs. The PINL has been deployed across six representative ICSs. The y-axis is the time step, with each ICS having a distinct time step length based on its control accuracy requirements, while the x-axis represents the standardized values of variables in ICSs. (a) The prediction and anomaly detection capabilities of the PINL. The second and third columns display the predicted state variables from the digital space and the actual measured values from the ICSs, respectively. The fifth column is the calculated mean absolute percentage error (MAPE) for the prediction results. The final column reports the F1-score for anomaly detection, quantifying the DT's accuracy in distinguishing between normal and abnormal operational states. (b) The decision-making efficacy of the PINL. |
| In the text | |
 |
Figure 4 The performance of PINL in the context of motor speed control system. The blue line represents the predictions and inferences generated by PINL, while the orange line reflects the data collected from the ICS. The time step is set to 0.05 s, aligning the controller's sampling rate with this interval. The first column displays normal conditions in the absence of any internal faults or external intrusions. The second column depicts a scenario where a fault in the speed sensor results in a deviation from the actual value. The remaining three columns verify the performance of PINL under cyber attacks. |
| In the text | |
 |
Figure 5 Evaluation of PINL's performance. (a)–(c) Effects of the integration of the structural knowledge on the performance of PINL. When no prior knowledge is available, i.e., model-free digital twin (MFDT), the structural code A is randomly generated to construct the graph skeleton. (d) Effects of network size on training time obtained from 20 trails across various ICSs. (e)–(h) Comparisons with representative machine learning-based DTs. (e)–(g) Accuracy comparison in prediction, decision-making, and anomaly detection. The proposed PINL scheme achieves comparable accuracy in capturing system dynamics and control policies in contrast to FNN-DT and STGNN-DT. (h) Model training time. A longer training time indicates greater computational demands and a lengthy testing process for parameter adjustments. Notably, the PINL has the least training time, underscoring its potential for practical implementation in ICSs with minimal effort. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.

